Spectacle Optics Help Documentation

By Darryl Meister

Revised 01 May 2010

This is online help documentation for the Spectacle Optics suite of optical design and analysis tools.

Program Installation

The program file is available for download here. Download the program to disk, unzip the program files, run the setup.exe program file to install the software, and then find the actual program short-cut to start the actual program. The user can choose between six different optical analysis modules.

Optical Analysis

Lens geometry is calculated for the specified lens, including the center thickness, edge thickness, weight, plate height, and weight. Peripheral or off-axis optical performance is calculated for the specified angle of ocular rotation, including the tangential power error, sagittal power error, oblique astigmatism (that is, tangential error − sagittal error), mean power error (that is, ½ tangential error + ½ sagittal error), rotatory distortion, and lateral chromatism, using Jalie's ray-tracing sequence. A vertical cross-section of the lens is also displayed along with the position of the eye. Additionally, a graph of the tangential (T) and sagittal (S) power errors is displayed, indicating the off-axis performance at intersection points across the entire back surface of the lens.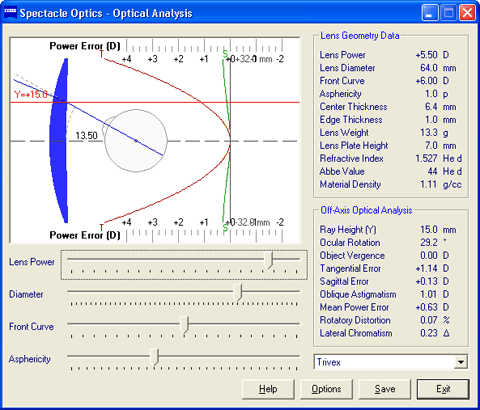

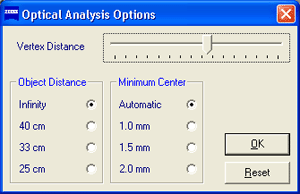
1. Set the back vertex power of the lens using the Lens Power slider control. Powers from −12.00 to +8.00 D can be selected.
2. Set the diameter of the lens using the Diameter slider control. Diameters from 30 to 76 mm can be selected.
3. Set the front curve of the lens, in the refractive index of the lens material, using the Front Curve slider control. Front curve powers from −4.00 to +16.00 D can be selected.
4. Set the asphericity of the front lens surface using the Asphericity slider control. Asphericity eccentricity values from −10.0 to +20.0 can be selected.
5. Set the lens material from the Material drop-down list.
6. Click and drag the red horizontal vernier line to set the 'Off-Axis Optical Analysis' calculations to a specific point of intersection on the back surface (that is, ray height in millimeters) or to a specific angle of view (that is, ocular rotation in degrees).

Note that, in higher prescription powers, off-axis performance may become erratic at extreme viewing angles as the mathematics involved break down. These results should be disregarded.

From the Options menu, the following assumptions may also be changed:

• Vertex Distance. The vertex distance can be varied to assess the performance of the lens over a range of vertex distances from 5 to 20 mm. The default is 13.5 mm. The actual stop or center of rotation distance utilized in the optical analysis calculations is determined by adding 13.5 mm to this vertex distance.
• Object Distance. The object distance can be varied to assess the performance of the lens over a discrete range of viewing distances from 25 cm to Infinity. The default is Infinity. Reducing the viewing distance will also result in a near vision effectivity error through the center of the lens, which is the difference in vergence for finite object distances due to lens form.
• Minimum Center. The minimum center thickness of minus-powered lenses can be selected. The default is Automatic, which uses a 2.0 mm minimum for low-index lenses and a 1.5 mm minimum for high-index lenses.

The power of a correctly fabricated spectacle lens will satisfy the intended prescription requirements in the vicinity of the optical axis of the lens. Within this area, which is referred to as the paraxial region, the angles of refraction involved are small and light behaves according to the simplified or first-order approximations of Gaussian optics. When viewing object points through the periphery of a spectacle lens, however, the angles of refraction become large and begin to diverge significantly from their small angle approximations. In this case, the effective focal power of through the tangential meridian (that is, the radial plane from the optical axis) may differ from the power of the lens through the sagittal meridian (that is, the plane a right angle to the tangential plane at any position on the lens). When the tangential and sagittal powers differ, an astigmatic focus is formed instead of a single point focus, resulting in two focal lines perpendicular to each other.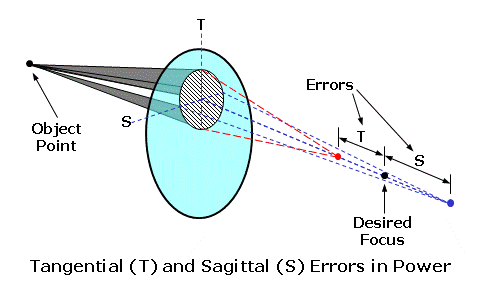

The difference between the tangential and sagittal focal powers, which is essentially equal to the amount of cylinder power between the tangential and sagittal meridians, is referred to as oblique astigmatism; this aberration is analogous to an error in prescribed cylinder power. The average dioptric distance of the tangential and sagittal from the ideal image plane of the eye, or far-point sphere of the eye, is referred to as the power error or mean oblique error; this aberration is analogous to an error in prescribed sphere power. These lens aberrations can be reduced or eliminated by varying the form, or relationship between the front and back curves, of the lens by selecting the appropriate base (or front) curve.

Alternatively, the use of asphericity can neutralize the oblique astigmatism produced by the lens through the use of surface astigmatism, which introduces a progressively increasing difference in tangential and sagittal curvature away from the center of the lens. This difference in curvature can offset the difference in focal power at a given angle of view. This allows flatter, thinner lens forms to be utilized without compromising peripheral optical performance. Aspheric surfaces often reduce the height of the lens surface as well, which further reduces either the center thickness of plus lenses or the edge thickness of minus lenses.

Chromatic aberration is the difference in focal power or prism between the blue end of the visible spectrum and the red end as a result of chromatic dispersion, or the breaking up of polychromatic (white) light as it passes through the material. Blue light has a higher refractive index than red light in transparent materials. Consequently, blue light is refracted more as it passes through a lens or prism, resulting in lateral chromatic aberration (or chromatism). This effect produces the familiar 'color fringing' that eyeglass wearers often experience in the periphery of high-index lenses. The dispersive property of a lens material is indicated by its Abbe value or constringence. Chromatic aberration is inversely proportional to the Abbe value, so lens materials with lower Abbe values produce more chromatic aberration.

Asphericity defines the relative eccentricity of a range of conic surfaces. Conic surfaces are produced by rotating a section of a cone about an axis of symmetry. A value of 1 defines a spherical surface; this is the default value. Values greater than 1 define oblate ellipsoidal surfaces that increase in curvature away from the center of the lens surface. These surfaces are particularly useful for minus-powered lenses that have been significantly flattened. Values below 1 define surfaces that decrease in curvature away from the center of the lens surface. Values between 1 and 0 define prolate ellipsoidal surfaces. A value of 0 defines a paraboloidal surface. Values below 0 define hyperboloidal surfaces.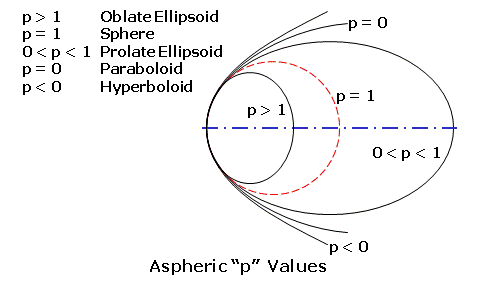

The lens cross-section and aberration plots can be saved as a bitmap image file. For more information, see Ophthalmic Lens Design.

| TOP |

Spectral Analysis

Spectral transmittance characteristics are calculated for the selected lens or filter, including the ANSI Z87 shade number, luminous transmittance, ANSI Z87 Blue-Light Hazard transmittance, ANSI Z80 ultraviolet A transmittance, ANSI Z80 ultraviolet B transmittance, the ANSI Z87 Blue-Light Hazard transmittance, and the reflectance of the base (that is, uncoated) lens material. Colorimetry values are calculated for the selected lens or filter, including the dominant hue, saturation purity, x chromaticity coordinate, y chromaticity coordinate, and z chromaticity coordinate in the CIE 1931 color space for the standard (2°) observer. The results are also displayed in four different charts.

1. Set the spectral output of the source using the Standard CIE Illuminant radio buttons. The selected illuminant will affect the color or tint of the lens as perceived by the wearer under a given lighting. The illuminant also establishes the white point of the color space. 'White' objects observed under an incandescent bulb, for instance, will appear more reddish than the same objects observed under natural daylight.
2. Set the lens or filter type from the Material drop-down list. A wide range of lens types is available, including tinted, specialty, and photochromic lenses.
3. Choose between four different charts 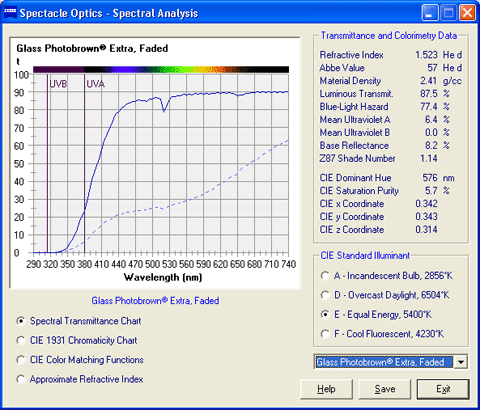to display the spectral transmittance or color characteristics of the selected lens or filter by selecting either the Spectral Transmittance, CIE 1931 Chromaticity, CIE Color Matching Functions, or Approximate Refractive Index radio buttons.

The Spectral Transmittance chart displays the spectral transmittance of the selected lens or filter as a function of wavelength or color across the visible, ultraviolet A (UVA, 315-380 nm), and ultraviolet B (UVB, 290-315 nm) spectra. Note that the luminous transmittance of the lens or filter is the spectral transmittance weighted by the photopic (that is, daylight) sensitivity or relative luminous efficiency of the eye. The eye is maximally sensitive to wavelengths near 555 nm during daylight viewing conditions; therefore, lenses that exhibit greater spectral transmittance near 555 nm also exibit a higher luminous transmittance.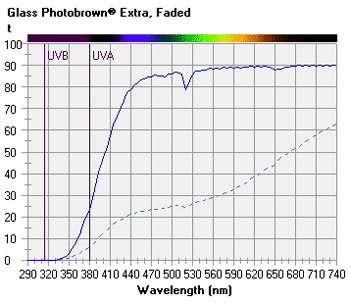

The CIE 1931 Chromaticity chart displays the dominant wavelength (or hue) and chromaticity coordinates of the lens or filter in the CIE 1931 color space based upon the selected illuminant. Quantities of three basic primary colors are required to produce a given color in an additive color system. In the CIE 1931 system, these quantities are represented by three tristimulus values, including an X value for red (at 700 nm), a Y value for green (at 546.1 nm), and a Z value for blue (at 435.8 nm). Each chromaticity coordinate represents the relative contribution of the corresponding tristimulus value, such that:

x = X ÷ (X + Y + Z)

y = Y ÷ (X + Y + Z)

z = Z ÷ (X + Y + Z)

The chromaticity coordinates of the selected lens or filter are plotted as a dark red cross. In this color space system, x + y + z = 1, so only two coordinates are required to define a given color (that is, x and y) when brightness is neglected.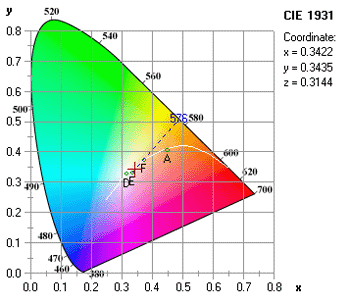

The CIE Color Matching Functions chart displays the three corresponding color matching functions of the lens or filter based upon the selected illuminant. The three color matching functions represent the relative quantity of each CIE primary color (red, blue or green) necessary for a 'standard' observer to match a given wavelength in the visible spectrum when viewed through the lens or filter. Note that the y-function is closely associated with the relative luminous transmittance of the lens, or the transmittance of the lens as weighted by the actual sensitivity of the eye to color.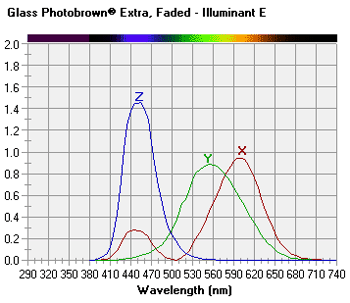

The Planckian locus is also plotted in white. This is the locus of color coordinates for a black body as its temperature is increased. For natural sources that produce light through incandescence, such as the sun and traditional light bulbs, the 'white point' of the source will follow this curve, passing from the lower-frequency reddish hues to the higher-frequency bluish hues of the color space, as the temperature increases. The temperature associated with each white point is referred to as the correlated color temperature.

A dominant wavelength line is also drawn from the white point of the selected illuminant through the chromaticity coordinates of the selected lens or filter. The wavelength at which the dominant wavelength line intersects the locus of pure spectral colors along the perimeter of the color space defines the dominant hue or color of the lens. The ratio of the distance between the white point and chromaticity coordinate to the distance between the white point and dominant wavelength defines the saturation (or excitation purity) of the lens. Note that, for a 'clear' lens, saturation will approach zero. Further, the dominant wavelength is not displayed for colors along the bottom purple boundary, between red and blue, since these colors represent non-spectral hues.

The Approximate Refractive Index chart displays the approximate refractive index of the lens or filter as a function of wavelength or color. The refractive index for each wavelength is calculated using the first two terms of a Cauchy polynomial. Because of the dispersive properties of transparent materials, blue light has a higher refractive index than red light. The dispersive property of a lens material is indicated by its Abbe value or constringence. Lens materials with lower Abbe values will therefore exhibit a greater difference in refractive index between the red and blue ends of the visible spectrum.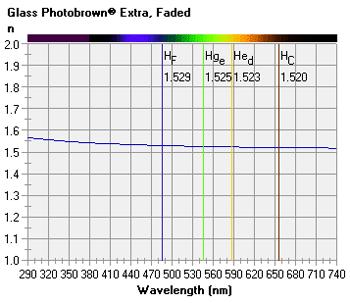

The reference wavelength used to calculate the 'stated' or mean refractive index of lens materials in the United States corresponds to the Helium (He) d Fraunhofer line at 587.56 nm. Some countries utilize a reference wavelength that corresponds to the Mercury (Hg) e line at 546.07 nm. The Abbe value is calculated using additional wavelengths corresponding to the Hydrogen (H) F line at 486.13 nm and the Hydrogen (H) C line at 656.27 nm, which represent the blue and red ends of the visible spectrum, respectively. The approximate refractive index values for these wavelengths are displayed. The Abbe value (ν) is related to the refractive index of the lens material for each of these three wavelengths (that is, He_d, H_F, and H_C) by:

ν = (He_d − 1) ÷ (H_F − H_C)

Each chart can be saved as a bitmap image file. For more information, see Spectral Transmittance and Color.

| TOP |

Prescription Analysis

A compensated prescription is calculated that corrects for the prescription optical effects of vertex distance, pantoscopic lens tilt, facial wrap (that is, face-form tilt), decentration, and vertical imbalance at the reading level (if any), along with the paraxial spectacle magnification for the manipulation of iseikonic lenses intended to reduce aniseikonia, or unequal image sizes. The lens centration geometry is also displayed in a lens centration diagram along with the approximate minimum blank size (MBS).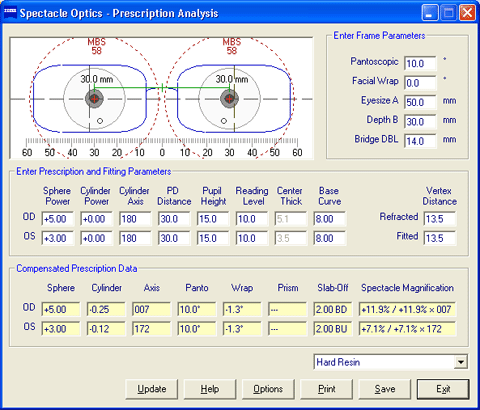

1. Set the frame parameters by filling out the Frame Parameters text fields. Pantoscopic tilt values from −35 to 35°, Facial Wrap values from −35 to 35°, Eyesizes (A measurement) from 20 to 80 mm, Depth (B) measurements from 10 to 60 mm, and Bridge (DBL) measurements from 5 to 30 mm can be selected.
2. Set the prescription and fitting parameters by filling out the Prescription and Fitting Parameters text fields. Sphere powers from −20.00 to +16.00 D, Cylinder powers from −7.00 to +7.00 D, monocular far interpupillary (PD) measurements from 20 to 40 mm, Pupil Height measurements from 5 mm to the maximum frame depth, Reading Level distances from 1 mm to the maximum frame depth, Center Thickness values from 1 to 25 mm, Base Curve values from −4.00 to +20.00 D, and Vertex Distance measurements from 0 to 30 mm can be selected.
3. Set the lens material from the Material drop-down list.
4. Click the Update button or tab out of any text field to update the 'Compensated Prescription Data.'

From the Options menu, the following assumptions may also be changed:

• Calculate Center Thickness Automatically. The center thickness of the lens can be calculated automatically. This is activated by default.
• Round Compensated Values to 0.12 D. The power and prism values can be rounded to the nearest eighth (0.12 D) diopter. This is activated by default.
• Use Prism Compensation for Wrap. The horizontal prism compensation as a result of face-form wrap can be activated or deactivated. This is activated by default.
• Optical Center Height. The vertical placement of the optical center can be selected. Choose At Datum 180° Line to place the optical center along the datum or mid-line (180°) of the frame, regardless of pupil height. Choose At Pupil Position to place the optical center at the height of the pupil. The default is At Datum 180° Line.

Note that, if the depth or 'B' measurement of the frame is changed, the Pupil Height value should be adjusted accordingly.

The layout geometry and pertinent data are displayed in a lens centration diagram. The location of the optical center of each lens is represented by a red cross. The location of the pupil center of each eye is represented by the center of each eyeball drawing. The vertical location of the reading level of each lens is represented by a small black circle. The outline of each lens diameter is represented by a dashed burgundy circle.

The optical effects of fitting geometry on the power of the lens as perceived by the actual wearer have been well documented. Increasing the vertex distance of a lens will result in an increase in plus power or a decrease in minus power. Conversely, decreasing the vertex distance will result in a decrease in plus or an increase in minus power.

Additionally, tilting a spherical lens will result in an increase in sphere power and the introduction of unwanted cylinder power of the same sign as the sphere power and oriented at an axis coincident with the axis of lens tilt (that is, at axis 90° for facial wrap and at axis 180° for pantoscopic tilt). Tilting a lens with cylinder power results in more complex optical interactions, particularly when both facial wrap and pantoscopic tilts are involved.

Tilting a lens also introduces an unwanted prismatic effect due to the thickness and curvature of the lens. For facial wrap, this prismatic effect results in unwanted horizontal prism imbalance, which can be eliminated through the use of horizontal prism of similar magnitude in the opposite direction. Further, even if the frame has no tilt, decentration of a meniscus lens, which occurs along an arc, will result in some degree of lens tilt.

Thin lens approximations are utilized to compute the prescription necessary in order to compensate for the effects of lens tilt. Please note, however, that the results of this prescription compensation apply only to single vision lenses. The results will be less accurate for progressive lenses (particularly lenses with prism-thinning), high-powered lenses, and lenses with prescribed prism, and should therefore be treated as merely informative.

The vertical prism imbalance at the indicated Reading Level is also calculated and displayed in the Slab-Off Prism fields for prescriptions with anisometropia. The default reading level is 10 mm. For prism imbalance values below 1.5 prism diopters, which is typically considered the threshold value for vertical imbalance compensation, the results are discarded. For prism imbalance values above 1.5 prism diopters, the vertical prism compensation at near is displayed for both lenses. For conventional slab-off grinding, choose the Base Up prism compensation. For reverse slab-off grinding, choose the Base Down prism compensation.

The centration diagram can be saved as a bitmap image file. The prescription form information can also be printed.

| TOP |

Geometrical Analysis

Image size and location (L') are calculated for the specified lens, mirror, or surface optical element with an equivalent power and object distance (L) from the center of the optical element set by the user. Linear magnification (×), or the ratio of the image size to the original object size, is calculated for a given pair of conjugate image and object distances. The numerical results are displayed along with a graphical representation of the ray tracing construction. The cardinal points of the optical element are calculated, including the primary focal and secondary points (F and F'), the location of the first and second principal points (P and P'), and the location of the first and second nodal points (N and N'). The location of each point along the optical or principal axis is also displayed relative to the origin (0) of the coordinate system, which represents either the physical center of the lens for lens optical elements or the pole of the surface for mirror and surface optical elements.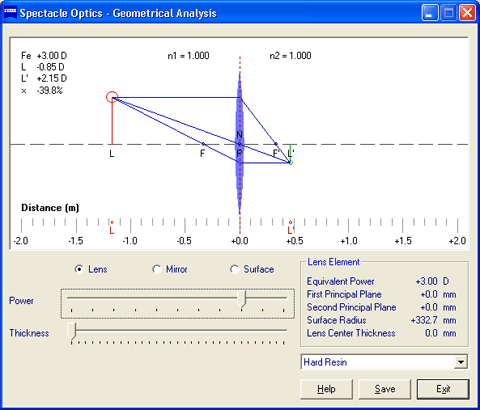

The equivalent power (F_E) of each optical element is equal to the vergence of the secondary focal point (F') at the plane of the second principal point (P') of the optical element. This also represents the image vergence produced by the optical element at the plane of the second principal point (P') for an infinitely distant object.

The object is displayed in red, and the image is displayed in green. Virtual objects and virtual images are displayed using dotted lines. The object (L) and image (L') locations are also displayed along the bottom scale. The following convention is utilized in the ray tracing construction:

• The scale represents the distance in meters either from the vertex of the optical element or from the center of the front and back vertices of lens optical elements of finite thickness.
• 'Object space' is on the left (negative) side of the optical element; objects in object space are real, whereas objects in image space are virtual.
• 'Image space' is on the righ (positive) side of the element; images in images space are real, whereas images in object space are virtual.
• Light travels from left to right.
• Although an optical element is displayed in each ray tracing construction, this is only for illustrative purposes; these optical elements are not drawn to scale.

1. Set the optical element type to ray trace using either the Lens, Mirror, or Surface radio buttons.
2. Set the equivalent focal power of the optical element using the Power slider control. Powers from −5.00 to +5.00 D can be selected.
3. Click and drag the red object to set the object distance for ray tracing.

For Lens optical elements: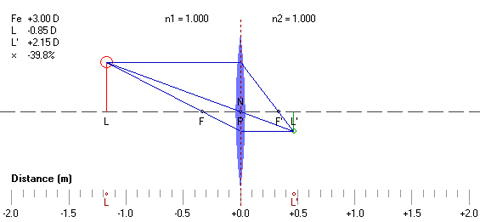

Either a biconvex (for plus power) or biconcave (for minus power) lens with equal front and back surface powers is defined based upon the specified equivalent power. The following additional variables may also be changed for lens optical elements:

• Set the center thickness of the lens element using the Thickness slider control. Thickness values from 0 to 150 mm, in 5 mm increments, can be selected.
Note that, because of the scale involved, center thickness may need to be large in order to see a noticeable difference in optical performance.
• Set the lens material from the Material drop-down list.

The front (left side) and back (right side) surface interfaces of the lens are both bounded by air (n₁ = n₂ = 1.000).

The equivalent focal power (F_E) of a lens optical element with a given refractive index (n), center thickness (t) in meters, front surface power (F₁), and back surface power (F₂) is given by:

F_E = F₁ + F₂ − t/n × F₁×F₂

Note that the equivalent power of a lens optical element of finite thickness will differ from the vertex power of the lens.

For Mirror optical elements: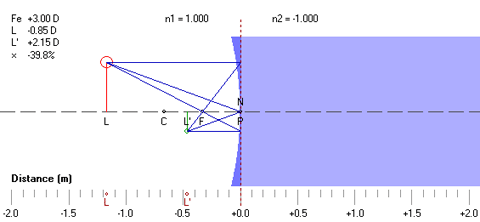

The mirror interface is bounded on the left side by air (n₁ = 1.000) and on the right side by a virtual reflection space equal to minus;n₁ (n₂ = −1.000).

The equivalent reflective power (F_E) of a mirror optical element with a radius of curvature (r) is given by:

F_E = −2×n₁ ÷ r

where n₁ = 1.000 in air.

For Surface optical elements: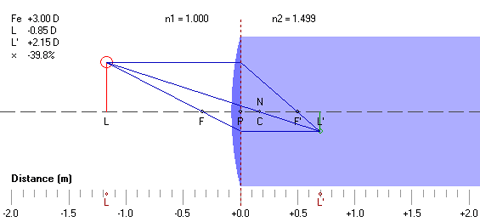

The following additional variable may also be changed for surface optical elements:

• Set the lens material from the Material drop-down list.

The surface interface is bounded on the left side by air (n₁ = 1.000) and on the right side by a medium with a refractive index equal to the index of the selected material (n₂ = n).

The equivalent refractive power (F_E) of a surface optical element with a given refractive index (n) and radius of curvature (r) is given by:

F_E = (n − n₁) ÷ r

where n₁ = 1.000 in air.

Three construction rays are drawn through each optical element in order to graphically construct the image:

1. The primary focal point ray is drawn from the object through the primary focal point to the first principal plane (P). This ray emerges from the second principal point (P') parallel to the optical or principal axis.
2. The secondary focal point ray is drawn from the object to the first principal plane (P) parallel to the optical or principal axis. This ray emerges from the second principal point (P') directed at the secondary focal point (F').
3. The 'undeviated ray' is drawn from the object through the first nodal point (N). This ray emerges from the second nodal point (N') at the same angle to the optical or principal axis.

Note that, when the object is placed to the right of the optical element or optical element interface, a virtual object (represented as a dotted line) results.

The principal points represent the conjugate object and image locations that result in unit (100%) linear magnification. Since these two planes are conjugate to each other, a ray of light directed at the first principal plane (P) will appear to exit the second principal plane (P') at the same distance from the optical axis, so that the action of the optical system on incident rays of light may be ignored between these two planes. The secondary focal point (F') of a 'thin' lens equal in power to the equivalent power (Fe) of an optical system will coincide with the secondary focal point (F') of the system when this thin lens is placed at the second principal point (P') of the system for measurements in image space. This thin, equivalent lens will also reproduce the linear magnification of the entire optical system when placed at the second principal point. Similarly, the primary focal point (F) of this same thin lens will coincide with the primary focal point (F) of the system when this thin lens is placed at the first principal point (P) of the system for measurements in object space.

The nodal points represent the conjugate object and image locations that result in unit (100%) angular magification. A ray of light directed at the first nodal point (N) will appear to exit the second nodal point (N') at the same angle to the optical or principal axis. The locations of the nodal points are equivalent to the locations of the principal points when the optical element is a lens bounded on both sides by a single medium or refractive index, such as air. A line passing through both nodal points of a lens intersects the optical axis at the optical center of the lens. The locations of both nodal points coincide with the location of the vertex of mirror optical elements. The locations of both nodal points coincide with the location of the center of curvature (C) of surface optical elements.

The ray tracing construction can be saved as a bitmap image file. For more information, see Ray Tracing of Thin Lenses.

| TOP |

Tscherning Analysis

The two best form front curves required to eliminate either the oblique astigmatism or mean power error aberration are calculated across a range of prescriptions. A graph of these front curves as a function of focal power is also displayed; this graph is commonly referred to as Tscherning's ellipse. These calculations assume that the lens is infinitely thin.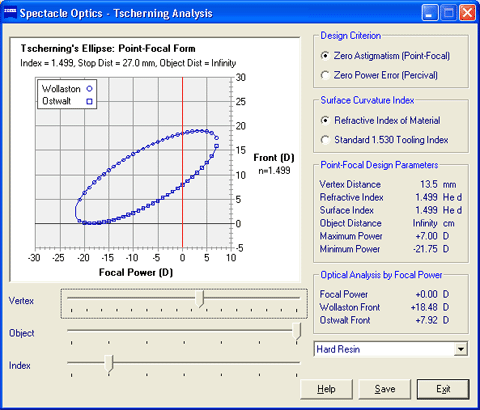

1. Set the Design Criterion using either the Zero Astigmatism (Point-Focal) or Zero Power Error (Percival) radio buttons. Point-focal forms correct for oblique astigmatism, whereas Percival forms correct for mean power error and are generally flatter than point-focal forms for a given focal power.
2. Set the Surface Curvature Index of the front curves using the radio buttons. To plot the front curves in the 1.530-based surface power used by laboratories choose Standard 1.530 Tooling Index. To plot the front curves in the actual refractive index of the lens material choose Refractive Index of Material.
3. Set the vertex distance of the lens using the Vertex slider control. Vertex distances from 5 to 20 mm can be selected. Adjusting this parameter will demonstrate the effects of vertex distance on lens design requirements. The actual stop or center of rotation distance utilized in the optical analysis calculations is determined by adding 13.5 mm to this vertex distance.
4. Set the object distance of the lens using the Object slider control. Discrete object distances from 20 cm to optical infinity can be selected. Adjusting this parameter will demonstrate the effects of object distance on lens design requirements. Note that, as the object distance is reduced, the ellipse expands down; therefore, flatter front curves are often preferred for near-vision-only lenses.
5. Set the refractive index of the lens material using the Index slider control or, alternatively, set the lens material from the Material drop-down list to choose a specific lens material. Refractive indices from 1.400 to 2.000 can be selected. Adjusting this parameter will demonstrate the effects of refractive index on lens design requirements. Note that, since high-index materials produce more surface power for a given physical curvature than standard materials, setting the Surface Curvature Index radio button to Standard 1.530 Tooling Index will provide a more uniform assessment of physical steepness or appearance when changing the refractive index.
6. Click and drag the red vertical vernier line to set the 'Optical Analysis by Focal Power' calculations to a specific focal power.

In 1804, William Wollaston invented a series of steeply curved spectacle lenses that eliminated oblique astigmatism. In 1898, Franz Ostwalt invented a flatter series of curved spectacle lenses that eliminated oblique astigmatism. In 1904, Marius Tscherning demonstrated mathematically that were two solutions to the same quadratic equation for the elimination of oblique astigmatism in a thin lens. Wollaston's steeper lens forms represented the negative solution of this equation and Ostwalt's flatter lens forms represented the positive solution. A plot of these two lens forms across the full range of valid focal powers is referred to as a Tscherning's ellipse.

'Best form' or 'corrected curve' spectacle lenses that eliminate oblique astigmatism (that is, tangential error − sagittal error) are referred to as point-focal lenses. 'Best form' lenses that eliminate mean power error (that is, ½ tangential error + ½ sagittal error) are referred to as Percival lenses after Archibald Percival, who first proposed eliminating mean power error in order to place the circle of least confusion of the oblique astigmatism focus at the far point of the eye.

The Tscherning ellipse plot can be saved as a bitmap image file. For more information, see Ophthalmic Lens Design.

| TOP |

Progressive Analysis

Optical performance is calculated for the specified progressive lens at each point across the surface, including the mean power, astigmatism, astigmatism axis, skew distortion, Zernike coma, Zernike trefoil, total Zernike high-order aberration, and prism magnitude. A contour plot of the selected optical distribution is also displayed. Additionally, a graph of the addition power as a function of vertical position along the umbilic of the lens surface is displayed.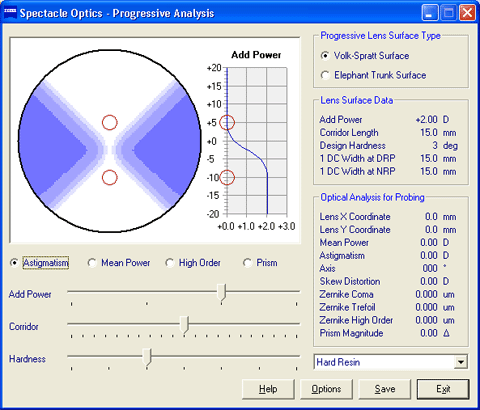

1. Set the contour plot to view using either the Astigmatism, Mean Power, High Order, or Prism radio buttons.
2. Set the lens design type using either the Progressive Lens Surface Type radio buttons. The umbilic of each surface is defined by the addition power, corridor length, and hardness. The Elephant Trunk Surface is created by applying circular cross-sections through each horizontal meridian that are equal in curvature to the vertical curvature of the umbilic at that point. This simple progressive lens design is similar in performance to many early progressive lenses. The Volk-Spratt Surface is created by crossing two identical surfaces at a right (90°) angle to each other, each with no horizontal change in curvature and a vertical change in curvature corresponding to the umbilic at each point. These two identical surfaces are essentially 'progressive' cylinders, which have a vertical progression of addition power but no horizontal change in power. The Volk-Spratt progressive lens design is similar in optical performance to many modern progressive lenses.
3. Set addition power of the lens using the Add Power slider control. Addition powers from +0.00 to +3.00 D can be selected.
4. Set the corridor length of the lens using the Corridor slider control. Corridor lengths from 5 to 25 mm can be selected.
5. Set the hardness of the lens using the Hardness slider control. Hardness values from 1 to 7 degrees can be selected. Hardness refers to the maximum order of the polynomial used to define the progression of addition power along the umbilic of the lens. Higher values of hardness will produce more rapid variations in addition power in the vicinity of the distance and near reference points.
6. Set the lens material from the Material drop-down list.
7. Move the mouse point over the contour plot to set the 'Optical Analysis for Probing' calculations to a specific point across the lens surface.

From the Options menu, the following parameters may be changed:

• Activate Manual Probing on Mouse Click. When activated, click on the contour plot to fix the results of the 'Optical Analysis for Probing' calculations at a single point; a red cross will appear at the selected point. When deactivated, the results of the 'Optical Analysis for Probing' calculations are updated as the mouse pointer is moved over the plot.
• Show Vectors over Plots. Vectors (represented by green lines) can be displayed for the astigmatism and prism contour plots, indicating the magnitude and orientation of these quantities at the indicated points. Vector values above 15 diopters are not displayed due to the length of the lines involved.
• Zernike Pupil Size. The diameter of the pupil used to calculate Zernike high-order aberrations can be selected from three typical sizes. The default is 6 mm. Zernike high-order aberrations will increase with larger pupil diameters.

The Astigmatism plot indicates the distribution of unwanted cylinder power across the lens surface in diopters (D).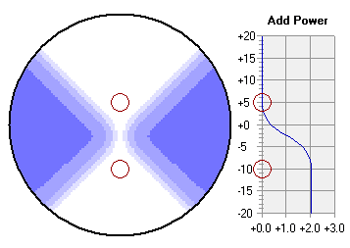

The Mean Power plot indicates the distribution of mean power or the spherical equivalent of the addition power across the lens surface in diopters (D).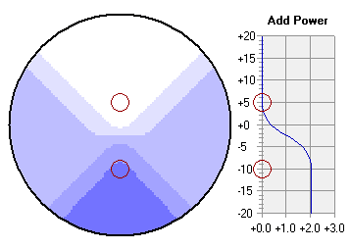

Progressive lenses produce a change in addition power without any visible lines of demarcation by blending the curvature of a flatter distance zone into a steeper near zone using plus-cylinder power oriented at an oblique axis. The use of plus-cylinder produces surface astigmatism and unwanted cylinder power in the periphery and over much of the lens surface. There is, however, a vertical line passing through the center of the viewing zones and the progressive corridor that is free from unwanted surface astigmatism, which is referred to as the umbilic of the lens surface. In the vicinity of the umbilic, the relationship between the increase in unwanted surface astigmatism and the change in addition power is dictated by Minkwitz's theorem, which states that increase in unwanted surface astigmatism away from the umbilic of the progressive corridor is proportional to the rate of change in addition power along the umbilic:

Astigmatism Change Lateral to Umbilic = 2 × Addition Change Along Umbilic

The rate of change in mean addition power is proportional to the addition power of the lens and inversely proportional to the corridor length of the lens. Therefore, progressive lenses with higher addition powers or shorter corridor lengths produce more rapid changes in unwanted surface astigmatism away from the umbilic of the lens surface as a consequence of Minkwitz's theorem.

The High Order plot indicates the distribution of RMS (root-mean-square) Zernike third-order coma and trefoil across the lens surface in microns (mm or 0.001 mm). Due to the variations in mean power and astigmatism that occur over a finite pupil aperture with progressive lenses, these lenses may produce non-negligible levels of certain 'high-order' wavefront aberrations, including the third-order Zernike aberrations of coma and trefoil. The High Order distribution represents the RMS, or root-mean-square, distribution of these Zernike third-order aberrations. The RMS distribution is equivalent to the standard deviation of the wave error.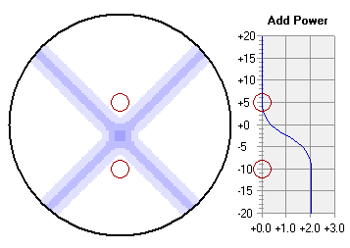

The Prism plot indicates the distribution of total prism (that is, the vector magnitude of the horizontal and vertical prism components) across the lens surface in prism diopters (D).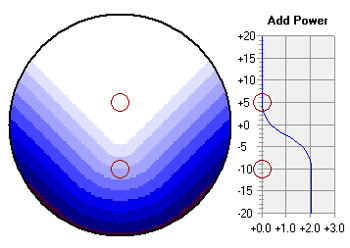

The selected contour plot can be saved as a bitmap image file. For more information, see Optics of Progressive Lenses.

| TOP |

Disclaimer

This software is intended for educational purposes only, and in no way represents the advice or direction of a licensed professional. Always use judgment when interpreting these results. This software is provided with no warranty, and by utilizing this software the user agrees to hold the author and Carl Zeiss Vision harmless from any liability or legal action that may result from its use.

Trademarks

• Transitions is a registered trademark of Transitions Optical, Inc.
• Photogray and Photobrown are registered trademarks of Corning, Inc.
• Spectralite is a registered trademark of Carl Zeiss Vision International GmbH
• CR-39 and Trivex are registered trademarks of PPG Industries, Inc.
• EYRY is a trademark of HO