 |
 |
|
|
Nature of LightBy Darryl Meister IntroductionThis course will present the fundamental principles of light and its interaction with objects, including a review of the visible spectrum, Snell's law of refraction, prism, and reflection. This is a technical, intermediate level course intended for dispensing opticians, laboratory technicians, and paraoptometric personnel. An understanding of basic mathematics is required. Historical PerspectiveSince the time of Plato, scientists have theorized about the exact nature of light. The renowned physicist, Isaac Newton, proposed that light consisted of streams of minute particles that were emitted from a source. He called these particles corpuscules, and his theory the corpuscular theory of light. This theory proposed that light exhibited particle-like nature. In the late 1600s, Robert Hooke and Christian Huygens each suggested that light emanated from a source in the form of waves, much like ripples across a pond. This has become known as the wave theory of light, and suggested that light exhibited wave-like behavior. At least one of these two theories could be applied to explain the various phenomena produced by light. Still, neither of them was able to explain completely every aspect of the complex behavior of light. Electromagnetic RadiationScientists broke further ground in the 1800s when Thomas Young was able to substantiate the wave nature of light with his "double-slit experiment." Another milestone came a few years later when James Maxwell suggested that light was, in fact, a form of electromagnetic radiation. Maxwell discovered that certain types of energy traveled through space via waves of electromagnetic radiation that vibrate along their direction of their travel (or propagation). These continuous waves of electromagnetic radiation are formed by continuously changing magnetic fields that vibrate perpendicularly to changing electrical fields. Waves of electromagnetic radiation travel at a speed of approximately 300,000 kilometers per second (186,000 miles per second) in free space. This discovery integrated the wave theory of light with the principles of electromagnetism. 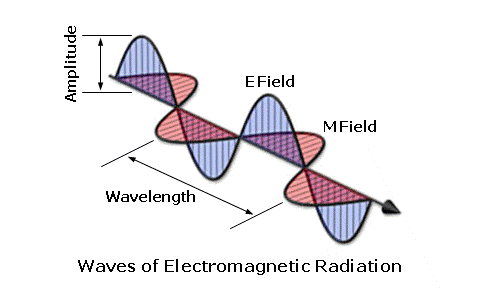 These waves are periodic, since they repeat at regular intervals (or cycles). The distance from crest to crest (or trough to trough) between any two waves is known as the wavelength. The height of the wave is known as the amplitude. Frequency describes the number of vibrations of the wave per unit length of time, or how fast the wave repeats itself. If we know the velocity (that is, 300,000 km/s) and wavelength of an electromagnetic wave, we can determine its frequency using: Frequency = Velocity ÷ Wavelength Consequently, the frequency of an electromagnetic emanation is inversely proportional (or inversely related) to its wavelength, and vice versa. This inversely proportional relationship means that, as the wavelength increases, the frequency decreases—and vice versa. Frequency is usually measured in cycles per second, or Hertz. Quantum TheoryAlthough the electromagnetic wave explanation of light seemed to be the most complete, it still failed to account for certain effects produced by light, like the photoelectric effect. In the early 1900s, Max Planck hypothesized that radiation wasn't simply produced in continuous waves of energy by the source, but rather discrete (or individual) packets of energy that he called quanta. A few years later, Albert Einstein extended Planck's quantum theory to light, and called these packets—or particles—of energy photons. Einstein proposed that light consisted of streams of these high-speed energy particles. The energy of a photon is directly proportional (or directly related) to its frequency; so electromagnetic radiation with a higher frequency also has a higher energy level: Energy ~ Frequency Consequently, if we know the frequency of a wave of light we can determine the energy of its photons. The total energy produced by waves of light will also be determined by the number of photons present, which is related to the amplitude of the light wave and its intensity. You can think of this relationship as Intensity of Light = Amplitude of Wave = Number of Photons. In essence, this new theory of light, which employed particles of energy called quanta or photons, was simply another form of the earlier corpuscular theory. Today, we say that light has a dual nature, with both particle-like and wave-like properties. Essentially, light consists of high-speed particles of energy—or photons—that travel in a wave-like manner. Light Interaction with ObjectsLight is emitted by a luminous—or primary—source, which is a source of energy that can generate visible radiation. This radiation is often produced by heat, and such sources include the sun, incandescent light bulbs, fire, and so on. Most other objects are visible because they reflect light from luminous sources. These objects are called secondary sources. When light is incident upon an object, the atoms in the surface of the object essentially "catch" its energy. At this point, the energy from the incident light can interact with the object in a variety of ways, and the three most common for lenses include:
For instance, consider a typical ophthalmic lens with a slight tint. The surfaces of the lens will reflect about 8% of the total incident light. The tint of the lens may absorb another 20% of the incident light, converting it into heat—another form of energy. Finally, the remaining 72% of the incident light will be transmitted through the lens. 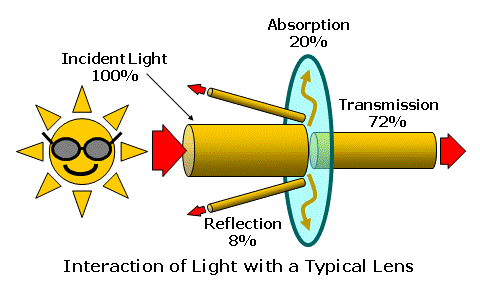 Other Wave PhenomenaAlthough less relevant to spectacle lenses, light can also interact with objects—particularly small objects—in other ways due to its wave-like behavior. Light can be diffracted, which is the subtle spreading (or bending) of light at the edge of an object or opening, particularly when the opening is small relative to the wavelength of light. Essentially, light waves reaching the edges of the opening act as new point sources for light waves continuing beyond the opening, allowing these waves to spread out as if they originated from the opening, itself. 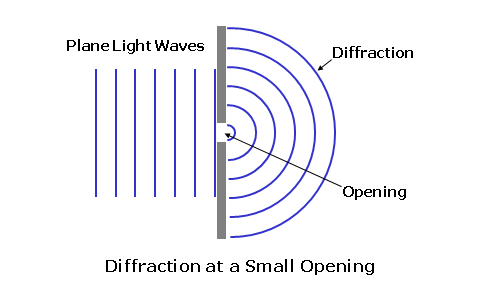 Light can also be scattered by objects that are small relative to the wavelength of light, redirecting it in many directions. When the particles are smaller than the wavelength of light, a phenomenon known as Rayleigh scattering occurs. The amount of light scatter produced by Rayleigh scattering is inversely proportional to the wavelength (or color) of light, so that blue light is typically scattered more than red light. This is why the sky appears blue; small particles in the atmosphere scatter blue light more than the other colors. Waves of light that reach the same place at the same time can also combine to form a new wave pattern without permanently disrupting each other, a phenomenon known as interference. When the peak of one light wave combines with the peak of another wave, the amplitudes of these two waves add to reinforce each other, resulting in in-phase or constructive interference. When the peak of one light wave combines with the trough of another wave, the amplitudes of these two waves subtract to cancel each other out, resulting in out-of-phase or destructive interference. Antireflection coatings rely on this phenomenon to reduce reflections by employing an optically thin layer of material that causes two separate waves to combine with each other after one wave has been offset in space from the other wave by one-half wavelength. This causes the peaks of the first wave to align with the troughs of the second wave, resulting in destructive interference, canceling the amplitude of the reflected light. 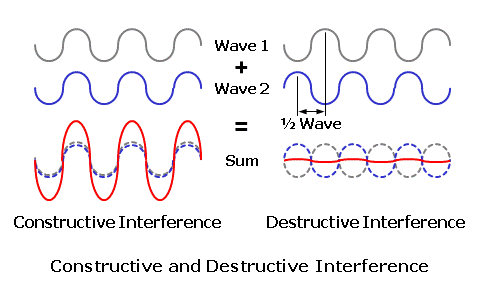 Visible Light and ColorThe spectrum of electromagnetic radiation includes cosmic rays at one end and radio waves at the other. We think of light as the visible portion of this electromagnetic spectrum. This means that the radiation can stimulate the photoreceptors within the retina of the eye, creating a visual sensation. This region consists of electromagnetic radiation whose waves range from 380 to 760 nanometers (nm)—or one billionth of a meter—in length. This is only 0.000380 to 0.000760 millimeters! The range of radiation visible to the human eye is referred to as the visible spectrum, ranging from violet at one end of the spectrum to red at the other, and represents a small fraction of the total electromagnetic spectrum. 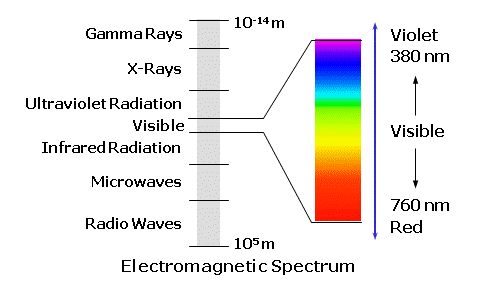 White light is composed of all the wavelengths in the visible spectrum. Individual wavelengths within the visible spectrum, by themselves, create different color sensations. These are the spectral colors. Remember that colors with shorter wavelengths, like blue and violet, have higher frequencies. Beyond the blue end of the visible spectrum lies ultraviolet radiation, while infrared radiation—which is often associated with heat—lies beyond the red end. These two forms of radiation are not visible to the human eye.
Recall that most objects are visible because they reflect light from luminous (primary) sources. For instance, you can see a red car down the road because it is absorbing every color of white light from the sun, except red. The color red is reflected off the car, which then serves as a secondary source for observers. Although white light from the sun is a continuous spectrum of colors, white light can be effectively reproduced by combining equal amounts of three specific colors of light: red, green, and blue. These colors are referred to as the additive primary colors, and any color from the visible spectrum can be reproduced by combining various quantities of these three colors of light. When no light is present, black (darkness) is produced. This is possible since the human eye only has three unique photoreceptors for color, called cones, which can each be stimulated by one of these three "primary" colors. This is concept is referred to as the trichromatic (three-color) theory of color vision. Consequently, equal amounts of red, green, and blue light will stimulate all three of these cones equally—just as white light from the sun would—giving the sensation of white. Television sets and computer monitors are common devices that use these three colors of light, in the form of excited phosphors, to produce a complete spectrum of colors. It is important to note that additive primary colors are produced by luminous or primary sources of light that emit colors. It is also possible to duplicate various colors of light by reflection, which is the basis for paint pigments and dyes. These would be secondary sources of light. The color black can effectively be reproduced by combining equal amounts of three specific colors: cyan, magenta, and yellow. These colors are referred to as the subtractive primary colors, and any color can be reproduced by combining various quantities of these three colors—which are often in the form of pigments or dyes.  These two sets of primary colors are also related in another way. Cyan is the "opposite" or complementary color of red, and is produced by combining blue and green. Magenta is the complementary color of green, and is produced by combining blue and red. Yellow is the complementary color of blue, and is produced by combining red and green. A color printer is a common device that use these three (subtractive) color pigments to produce a full range of colors. When no colors are present, the color is assumed to be white. It is interesting to note that the three particular paint pigments used in printing do not produce a perfect black so a fourth, perfectly black pigment is often used (which represents the 'K' in CMYK printing). Refractive IndexThe substance through which waves of light travel is referred to as the medium. Media can include empty space, air, lens materials, and so on. Recall that waves of light travel at a constant velocity of approximately 300,000 km/s in free space. In other transparent media, including lens materials, waves of light will travel at a slower rate. The velocity of light in other media will vary as a function of the refractive index for that material. The refractive index of a transparent medium is essentially a measure of the "optical resistance" of the material to light, and is defined as the ratio of the velocity of light in air compared to the velocity of light in the material: Refractive Index = Velocity in Air ÷ Velocity in Material For example, consider a wave of light traveling at a velocity of 200,000 km/s through a particular lens material. The refractive index for that lens material would be equal to 300,000 km/s ÷ 200,000 km/s = 1.500. The refractive index of a material is often abbreviated 'n.' Except for air, which has a refractive index of 1, the refractive index of most substances is greater than 1 (n > 1). Water, for instance, has a refractive index of 1.333. Spectacle lens materials are available in a variety of refractive indices, ranging from 1.497 to 1.886. Some common materials are shown below.
The higher the refractive index of a lens material, the slower the light will travel through it. In reality, the refractive index of any material varies slightly as a function of the wavelength. This means that various colors of light will each actually have a slightly different refractive index in the same lens material! This phenomenon is responsible for chromatic dispersion, or the breaking up of white light into its component colors by prisms and lenses. Blue light, which has a higher refractive index than red light, is refracted—or bent—more than red. 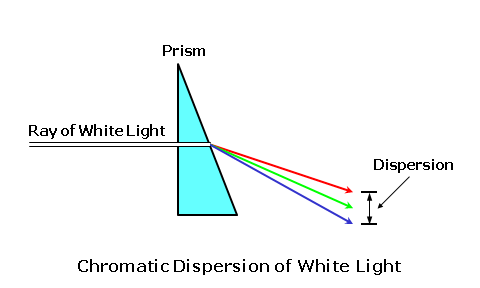 Chromatic dispersion is a result of the fact that colors of light with shorter wavelengths, like blue, travel more slowly through most transparent materials than colors with longer wavelengths, like red. Therefore, blue light generally has a higher refractive index than red light. However, this is usually only a concern for certain high-index lens materials, since the differences in refractive index between colors is more dramatic. Vergence of LightWhen light is emitted by a luminous source the radiation travels outward in a wave-like fashion. This is similar to a pebble creating ripples in a pond. Waves traveling across water are confined to one plane, the surface of the water, so they travel outward circularly. Light waves from a luminous point source, however, travel in every direction and form spherical wave fronts. Each wave front is like a spherical "shell" that envelops all of the waves at the same distance from the source. Each spherical wave front "expands" from the source, like a balloon gradually inflating with air. Since these wave fronts propagate (or travel) away from the point source of light, the source serves as their common center of curvature. Point A represents a source with waves of light propagating outward in every direction. The wave front is the spherical shell that envelops all of these waves at the same distance from the source. Line AB represents a ray originating from point A, the center. Any ray originating at the center of curvature of these waves will remain perpendicular to each wave front. Consequently, for simplicity, we can represent these wave fronts with simple rays (or lines) traveling through the medium in the direction of the original waves. 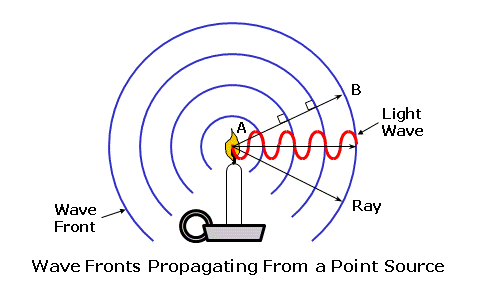 The notion that light can be thought of as traveling in straight lines is referred to as rectilinear propagation. Furthermore, in lens diagrams, rays of light are always depicted as initially traveling from left to right. Note that the rays are spreading apart as they travel away from their point source (the candle flame). When rays or wave fronts of light spread out from their point source, they are diverging. When rays or wave fronts of light come together and join or collapse to a point focus, they are converging. 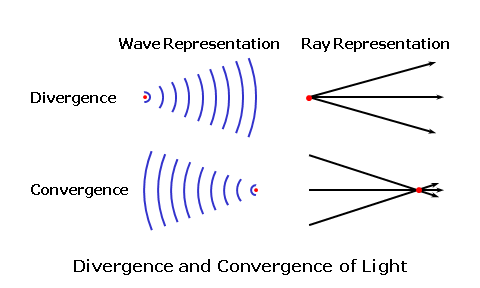 Since these spherical wave fronts expand as they travel from their source, the size of each spherical shell is directly related to its distance—or radius (r)—from the point source. The longer the distance from the source, the flatter the curvature of the wave front. Conversely, the shorter the distance from the source, the steeper the curvature of the wave front. 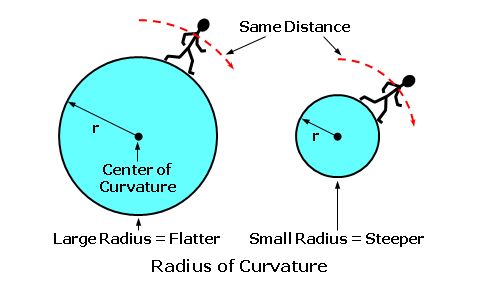 The curvature of the wave front of light, which describes both how steep or flat the wave front is and how far it is from its source or its focus, is referred to as its vergence. Vergence is measured in a unit called the diopter (abbreviated 'D'). In air, which has a refractive index of 1, the vergence of light at a given distance (in meters) is given by: Vergence = 1 ÷ Distance Consequently, a wave front will have 1.00 diopters (D) of vergence at a distance of 1.0 meter (m). This formula shows that vergence is inversely proportional to either the distance from the source (for diverging light) or the distance to the focus (for convergering light): As the distance increases, the vergence decreases—and vice versa. Furthermore, when rays of light are diverging the vergence is generally considered negative (-), and when rays are converging the vergence is generally considered positive (+). 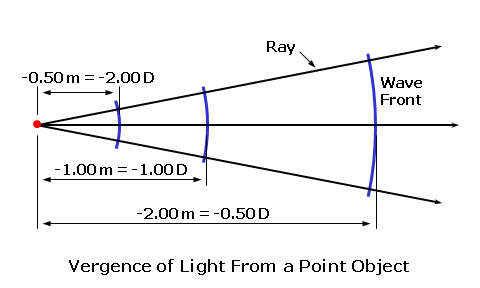 For example, consider light rays diverging from a book at a distance of 16" (0.40 m) from the eyes, which is a typical reading distance (since the light is diverging, we'll use a negative value). The vergence at the eyes is equal to 1 / -0.40 = -2.50 D. Wave fronts get flatter and flatter as they get farther from their source. At some distance, the wave fronts will appear to be perfectly flat and nearly parallel with each other. The rays of light representing these wave fronts—and perpendicular to them—will also appear to be parallel with each other. This distance is called optical infinity, and is usually assumed to be 6 meters in ophthalmic optics. Therefore, rays of light from an infinitely distant object are always drawn parallel to each other. Refraction of LightWhen light travels from one medium into another with a different refractive index, the velocity of the light will change. When going from a lower-index medium to a higher-index medium that is more optically dense, such as from air to a piece of glass, the velocity is reduced. If the rays of light are incident upon the glass surface perpendicularly, or at a 90° angle to the surface, the rays will pass through without changing direction. When rays of light strike a different medium obliquely, or at an angle, they are refracted, or bent, at the boundary (or interface) between the two media. When going from a lower-index medium to a higher-index medium that is more dense, such as from air to a piece of glass, the rays of light are shifted toward the normal, which is an imaginary line of reference perpendicular to the surface at the point of incidence. When going from a higher-index medium to a lower-index medium that is less dense, such as from a piece of glass to air, the reverse occurs and the rays of light are shifted away from the normal of the surface. This process can be better visualized by considering the wave form of light. Wave fronts entering the glass medium perpendicularly are slowed down uniformly, but there is no change in their direction. Now consider wave fronts entering the glass obliquely... Side A of the approaching wave fronts strikes the glass before side B, causing side A to slow first. As a result, the waves are refracted, or bent, toward the slower side as they enter the medium. The opposite situation occurs when the wave fronts exit the glass. 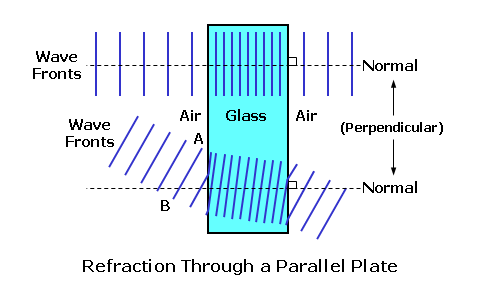 If the glass slab has parallel faces, the waves of light will emerge from the other side parallel to their original path, but slightly displaced. We can also consider the principle of refraction using a common analogy... Consider a car (the light) driving along a smooth highway (the air). If the right passenger side of the vehicle strays into the rough shoulder (the lens material) adjacent to the road, the right side of the vehicle starts to drag. Consequently, since the left side of the vehicle is traveling faster than its right side, the vehicle veers towards the shoulder (or material). 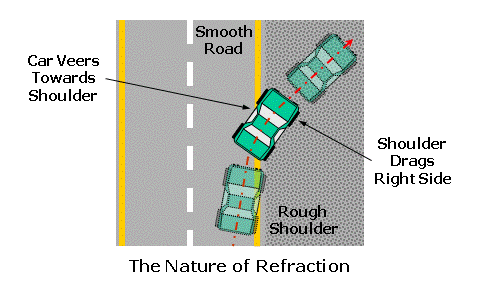 Wave fronts refracted through an "optical element" (such as a lens or prism) with parallel faces (such as a glass slab) will emerge parallel to their original path, but slightly displaced. The amount of displacement will depend upon the refractive index and thickness of the slab. Consider a ray of light traveling from one medium, such as air, into another medium with a differing refractive index, such as a lens material. The ray of light will be refracted at the boundary between these two media as it passes from the first medium into the second medium, if it strikes the boundary at an angle. Snell's law of refraction is used to determine how much refraction (or bending) occurs as light passes through the boundary between two media with different refractive indices, and is fundamental to the study of optics. To use Snell's law, we will fist label the refractive index of the first medium as (n) and the refractive index of the second medium as (n'). We will then label the angle of incidence (i) in the first medium, which is the angle between the initial, incident ray of light and the normal to the boundary interface (that is, a line perpendicular to the surface). Lastly, we will label the angle of refraction (i'), which is the angle between the refracted ray of light and the the normal to the boundary interface. Snell's law tells us that the product of the sine of the angle of incidence (i) and the refractive index (n) of the first medium is equal to the product of the sine of the angle of refraction (i') and the refractive index (n') of the second medium. Mathematically, Snell's law is given by: n × sin i = n' × sin i' Both the angle of incidence and the angle of refraction are measured from the normal, the imaginary reference line perpendicular to the surface or boundary at the point of incidence. 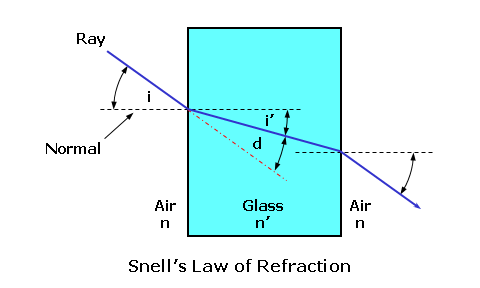 A third angle, the angle of deviation (d), lies between the refracted ray and the direction of its original path. This angle represents the shift of the ray from its original path. Consequently, the angle of deviation is equal to the difference between the angles of incidence and refraction, or d = i - i'. Recall that as the ray passes back into the lower-index medium, it is again deviated—this time, away from the normal. Snell's law mathematically establishes how much rays of light will be deviated from their original paths as they pass between various media. The greater the difference between the refractive indices of the two media, the greater the amount of refraction. Reflection of LightIt was mentioned earlier that we see most objects simply because light "bounces off" them. More specifically, some of the light is absorbed by the surface of an object and then re-emitted backwards. This process is known as reflection. The amount and color of light reflected from an object will depend upon the nature of the reflecting material and the angle that the light strikes it. Reflection can be described with a simple relationship, known as the law of reflection, which states that the angle of incidence (i) of the incident light is equal to the angle of reflection (r) of the reflected light. Mathematically, the law of reflection is given by: i = r Or, Angle of Incidence = Angle of Refraction As with refraction, both angles are measured from the normal to the boundary (that is, a line perpendicular to the surface). This concept is analogous to a ball striking a wall at an angle and bouncing off that wall at the same angle. There are two primary kinds of reflection:
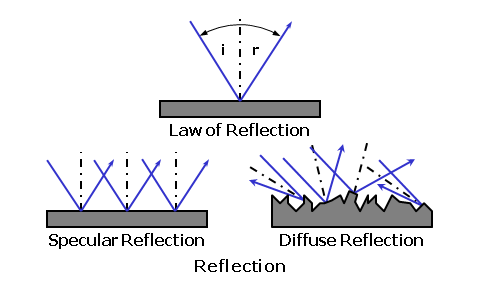 Mirrors are a common example of specular reflection; the source of the reflected light is still visible from the mirror because the orderly reflection creates an image. No image is created by diffuse reflection. Some degree of reflection generally occurs at the boundary (or interface) between two different refractive media, such as air and glass. The fraction of incident light that is reflected is known as the reflectance. For light reaching the interface between two different media with refractive indices of (n) and (n'), the reflectance is given by Fresnel's formula: Reflectance = (n - n')2 ÷ (n + n')2 To express the reflectance as a percentage, simply multiply it by 100. Consequently, as the refractive index of the lens material increases, the amount of light reflected increases. In reality, the actual amount of reflectance between two media will depend upon the initial angle of incidence at their boundary. For example, consider light that is incident upon a transparent medium with a refractive index of 1.500, surrounded by air (with a refractive index of 1). The reflectance is equal to (1.500 - 1)2 ÷ (1.500 + 1)2 = 0.04 (or 4%). Each surface of common glass and plastic lens materials reflects at least 4 to 5% of the light incident upon the lens. Between both surfaces, this represents a total reflectance of at least 8%. Conversely, a completely clear lens (with little or no absorption) can only transmit 92% of the light passing through it. Thin coatings can be applied to a lens surface to reduce this reflectance to almost nothing—thereby increasing the transmittance of the lens. Refraction by PrismsWe can now apply the concept of refraction to "optical elements" designed to manipulate light. One of the simplest optical elements is the prism, which is simply a wedge-shaped piece of refracting material. More specifically, a prism is a refracting medium bound by two non-parallel sides (that is, they are at an angle to each other). Like a triangle, the thickest edge of the prism is referred to as the base, while the thinnest edge of the prism is referred to as the apex. This wedge-shaped element changes the direction of light without necessarily changing its vergence. A prism displaces, or bends, light passing through it towards the base of the prism. This is the thicker end of the prism. In the simplest case, a ray of light strikes the first surface at a normal (perpendicular) incidence, and remains undeviated. Upon reaching the second surface, the ray is refracted away from the normal to the surface, according to Snell's law of refraction, and towards the base of the prism. 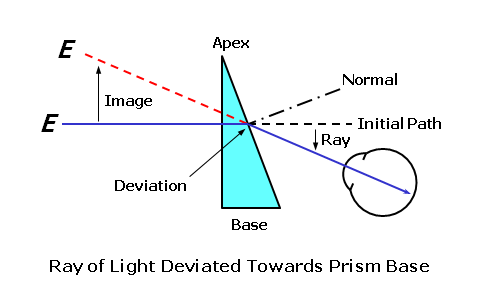 Although a prism displaces light towards its base, when the refracted light is projected backwards it makes the object appear as though it originated in the opposite direction of this displacement. Consequently, we say that the image created by a prism is displaced towards the apex of the prism. This point is extremely important and worth reiterating: A prism deviates light towards its base and images toward its apex.  For thin prisms, whose thickness and apical angles are negligible, the amount of displacement will depend upon the refractive index of the material and the apical angle of the prism, which is the angle of the apex or the "tilt" between the two faces of the prism. However, the approximate deviation produced by a thin prism, in degrees, can be determined using: Deviation = (Index - 1) × Apical Angle Consequently, the amount of displacement will depend upon both the refractive index of the material and the apical angle of the prism. Prisms with greater apical angles are "stronger" and will deviate light more. The approximate deviation (d) of the prism is equal to quantity (n - 1) times the apical angle (a). 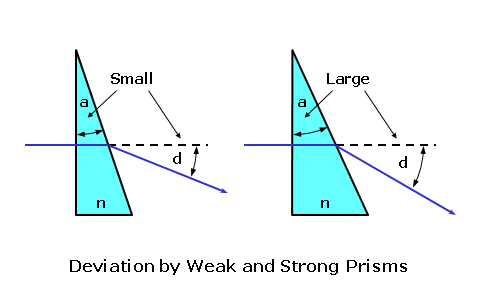 For example, consider a prism with an apical angle of 10° made in a material that has a refractive index of 1.500. The deviation is equal to (1.500 - 1) × 10° = 5°. In practice, the initial angle of incidence of the light reaching the first surface will also affect the total amount of deviation produced by the prism slightly. As a result, the exact formula for calculating prism is more complicated than this. Light and ShadowsWe will conclude our discussion of the basic properties of light by briefly reviewing shadow formation. Without light, we would only have darkness, which—strictly speaking—is the absence of light. When a region that would otherwise be illuminated is blocked from its light source, a shadow—or area of darkness—results. There are two categories of shadows:
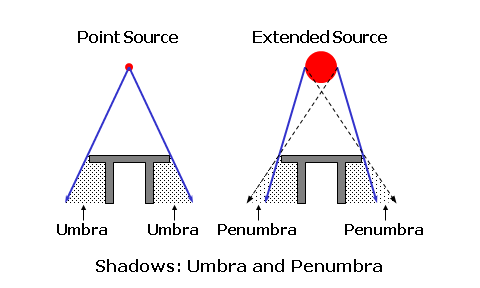 A penumbra occurs when only part of an extended light source is illuminating a region. In most cases, both an umbra (no illumination) and a penumbra (partial illumination) are formed. |

