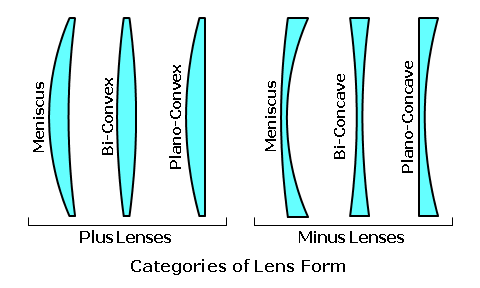
Ophthalmic Lens Design

By Darryl Meister

Introduction

This course will present the fundamental principles of ophthalmic lens design, including a review of lens aberrations, corrected curve theory, and asphericity. This is a technical, intermediate level course intended for dispensing opticians, laboratory technicians, and paraoptometric personnel. An understanding of both basic mathematics and basic optics is required.

Focal Power

The ability of a lens to refract and focus light—by either converging or diverging it—is referred to as its focal power or refractive power. The focal power of a lens is simply equal to the net effect of its front and back surfaces. When a refractionist writes a prescription for an ophthalmic lens, he/she is specifying the focal power of the lens. The focal power of a lens, in diopters, is given by:*

Focal Power = Front Surface Power + Back Surface Power

Or:

P = F + B

Where (P) is focal power in diopters, (F) is the front surface power in diopters, and (B) is the back surface power in diopters. Both focal power and surface power are measured in units called diopters (abbreviated 'D').

For example, consider a lens with a 6.00 D front curve and a -4.00 D back curve. The focal power (P) is equal to F + B = 6.00 + (-4.00) = +2.00 D.

* This is an approximation to keep our math simple; the formula becomes a bit more complex when lens thickness is considered.

Lens Form

The relationship between the front and back surface curves of a lens is referred to as the lens form (or lens profile). A lens with a given focal power can be produced by many different lens forms, as long as the sum of the front and back surface powers remains constant—or at least nearly so (neglecting thickness). A given lens power can be produced with an almost endless variety of lens forms, as long as the sum of the front and back surface powers remains equal to the desired focal power.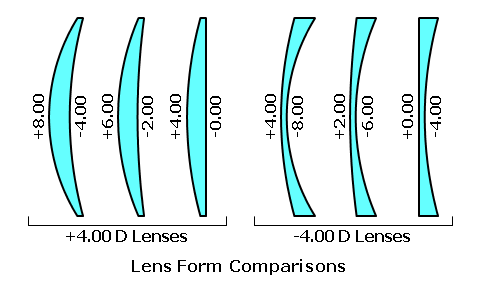

Historically, spectacle lenses fall into either one of two general categories of lens form:

• Bent lenses: Modern lens form are generally bent, or meniscus—which means "crescent-shaped." Bent lenses use convex front curves and concave back curves.
• Flat lenses: The earliest lens forms were flat. For plus lenses, flat lenses use either convex curves for both the front and back (i.e., bi-convex lenses), or one convex curve and one plano (plano) curve (i.e., plano-convex lenses). For minus lenses, flat lenses use either concave curves for both the front and back (i.e., bi-concave lenses), or one concave curve and one plano (plano) curve (i.e., plano-concave lenses).

Base Curve Selection

The form of a given lens is determined by "base curve selection." The base curve of a lens is the surface curve that serves as the basis or starting point from which the remaining curves will be calculated. For semi-finished lens blanks, the base curve will be the factory-finished curve, which is generally located on the front of the blank. The surfacing laboratory is ultimately responsible for choosing the appropriate base curve for a given prescription (or focal power) before surfacing the lens. For finished lens blanks, which have already been fabricated to the desired power, the curves are chosen beforehand by the manufacturer.

Manufacturers typically produce a series of semi-finished lens blanks, each with its own base curve. This "base curve series" is a system of lens blanks that increases incrementally in surface power (e.g., +0.50 D, +2.00 D, +4.00 D, and so on). Each base curve in the series is used for producing a small range of prescriptions, as specified by the manufacturer. Consequently, the more base curves available in the series, the broader the prescription range of the product. Manufacturers make base curve selection charts available that provide the recommended prescription ranges for each base curve in the series.

The base curve of a lens may affect certain aspects of vision, such as distortion and magnification, and wearers may notice perceptual differences between lenses with different base curves. Consequently, some practitioners may specify "match base curves" on a new prescription. Some feel that these perceptual differences should be minimized by employing the same base curves when the wearer obtains new eyewear. This would conceivably make it easier for particularly sensitive wearers to "adapt" to their new eyewear.

However, changes in the spectacle prescription will also create unavoidable perceptual differences. Moreover, the wearer will generally adjust to these perceptual differences within a week or so. If the same base curve is continually used as the wearer's prescription changes, which might necessitate a change in the manufacturer's recommended base curve, the peripheral optical performance of the lens may suffer as a consequence. When duplicating lenses of the same lens material, design, and power, matching base curves should not pose a problem—and is a recommended practice. Otherwise, unless the wearer has shown a previous sensitivity to base curve changes, you should use the manufacturer's recommended base curve when changing the prescription, or when using different lens materials and/or designs.

There are some exceptions to this rule, though they are rare. Some wearers with particularly long eyelashes may have been given steeper base curves at some point in order to prevent their lashes from rubbing against the back lens surface when their vertex distance—or the distance between the lens and the eye—is small, though this practice is very uncommon. Additionally, some wearers with a significant difference in prescription between the right and left eyes may suffer from aniseikonia, or unequal retinal image sizes, and require unusual base curve combinations in order to minimize the magnification disparity produced by the difference in lens powers. In these situations, a discussion with the prescriber may be in order before changing base curves.

Since the power of a lens can be produced by an almost infinite range of lens forms, why choose one base curve over another? There are two principal factors that influence the selection of base curves (and their resulting lens forms):

• Mechanical factors
• Optical factors

Mechanical Factors of Lens Form

The maximum thickness of a lens, for a given prescription, varies with the form of a lens. Flatter lens forms are slightly thinner than steeper lens forms, and vice versa. Since the lenses are thinner, they also have less mass—making them lighter in weight as well. In addition to lens thickness, varying the lens form will also produce significant differences in the plate height, or overall bulge, between lenses of the same power. Essentially, plate height is the height of a lens as measured from a flat plane.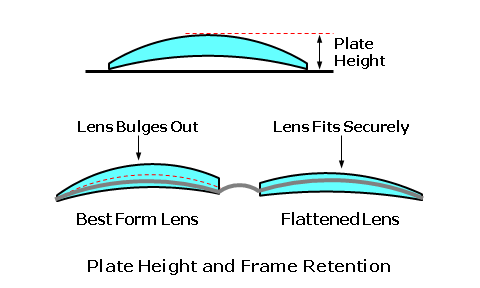

Plus lenses with flatter plate heights do not fall out of frames as easily, which is especially important with large or exotic frame shapes. In addition, flatter plate heights are also more cosmetically pleasing than steeper, bulbous ones—particularly in plus powers.

A reduction in plate height will also provide a significant reduction in the magnification associated with plus lenses. Since a flatter plate height brings the back surface closer to the eye, the minification associated with minus lenses is also reduced slightly. This gives the wearer's eyes a more natural appearance through the lenses.

We can evaluate the maximum thickness, plate height, and weight for a range of lens forms to demonstrate the effects of lens form upon cosmesis for a given prescription. The table, below, represents a range of +4.00 D lenses in hard resin plastic, edged to a 70-mm diameter and a 1-mm minimum edge thickness.

Note how the lenses become gradually thinner, flatter, and lighter in weight as the base curve is reduced—or flattened. The table, below, represents a range of -4.00 D lenses in hard resin, edged to a 70-mm diameter and a 2-mm minimum center thickness.

Again, the lenses become gradually thinner, flatter, and lighter in weight as the base curve is reduced. In summary, flatter lens forms provide the following mechanical and cosmetic benefits:

• Flatter (less "bulge")
• Thinner center thickness (plus) or edge thickness (minus)
• Lighter in weight
• Less magnification (or minification)
• Better frame retention (in plus powers)

Optical Factors of Lens Form

We've just discussed the obvious mechanical and cosmetic advantages of flatter lens forms (with their flatter plate heights). However, the principal impetus behind lens form selection is optical performance. Base curves are typically chosen to provide a wide field of clear vision. It turns out that the form of a lens will have a significant impact on the clarity of peripheral vision experienced by the wearer. Although vision through the center of a lens will be relatively sharp no matter what the form, vision through the periphery of a lens will vary greatly as a function of lens form.

Peripheral vision generally requires the wearer to look away from the optical center of the lens. As a result, the wearer's line of sight makes an angle to optical axis of the lens, which is the imaginary line passing through the optical center. Consequently, we often refer to the peripheral performance of a spectacle lens as its off-axis or off-center performance. During peripheral and dynamic vision, the line of sight makes an angle to the optical axis of up to 30° or more as the wearer observes objects in the visual field.

The focal power formula, P = F + B, adequately describes the behavior of the lens near its optical center, within an area referred to as the paraxial region, since incident rays of light make very small angles to its optical axis. These small angles result in a well-behaved refraction of the incident light rays, allowing us to simplify Snell's law of refraction using a mathematical simplification known as a first-order approximation. Light rays refracted through the paraxial region will form a sharp point focus at the desired focal point of the lens and ultimately upon the retina of the eye.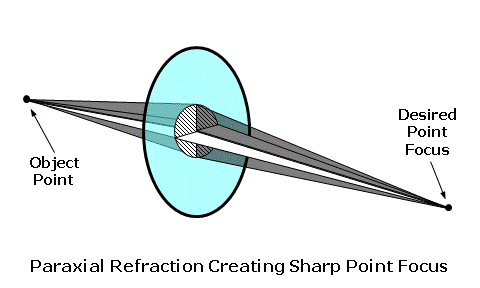

However, away from the paraxial region, the incident rays of light make larger and larger angles to the optical axis, and the first-order approximation no longer accurately describes the refraction of light rays. Incident rays of light are no longer brought to a single point focus at the desired focal point of the lens, as described by our simple focal power formula. This error in focus is referred to as a lens aberration.

Lens aberrations act as errors in power from the desired prescription, and can degrade the image quality produced by the lens as the wearer gazes away from—or obliquely to—its optical axis. There are six different lens aberrations that can affect the quality of peripheral vision through a spectacle lens:

• Oblique Astigmatism
• Power Error
• Spherical Aberration
• Coma
• Distortion
• Chromatic Aberration

The first five lens aberrations are referred to as the monochromatic aberrations, since they occur independently of color. They are also referred to as the Seidel aberrations, since Ludwig Von Seidel first derived equations for assessing these aberrations using a third-order approximation (which is more accurate than the first-order approximation). We will concentrate mainly on oblique astigmatism and power error, which are the two primary lens aberrations that must be reduced or eliminated when designing ophthalmic lenses.

The sixth lens aberration, chromatic aberration, is a consequence of the dispersive properties of the actual lens material, and is not a function of lens design.

You can also think of a lens aberration as the failure of a lens, which has otherwise been made correctly, to produce a sharp focus at the desired focal point of the lens as the eye rotates behind it in order to view objects in the periphery. The focal power of the lens is prescribed to produce a focus at the far-point of the eye. The far-point (FP) of the eye is conjugate to the retina, meaning that rays of light from a lens that come to a focus at the far-point will also be brought to a focus at the retina once refracted by the eye. Hence, the far-point represents the ideal focal plane of the spectacle lens.

As the eye rotates vertically and horizontally behind the lens, the far-point moves with the eye at a fixed distance from its center of rotation (C). This movement describes an imaginary spherical surface, known as the far-point sphere, which represents the ideal locus of focal points for the lens as the eye rotates to look through it. Lens aberrations result when light refracted by a lens fails to come to a focus at the far-point sphere.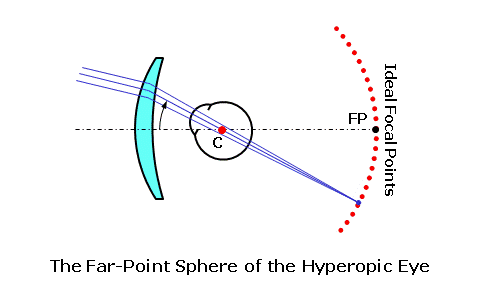

Tangential and Sagittal Errors

In our discussion of lens aberrations, we will often refer to the tangential and sagittal errors from the desired power. The tangential plane of the lens represents the meridian of the lens that radiates out from the optical center; these planes are analogous to the spokes of a bicycle wheel. The sagittal plane of the lens represents the meridian of the lens that is perpendicular to the tangential plane (i.e., at a 90° angle to it) at any point; these planes circumscribe the optical center.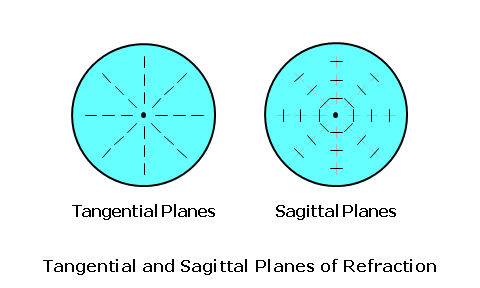

When rays of light from an object strike the lens obliquely, the principal refraction of these rays occurs through the tangential and sagittal meridians, much like the principal refraction of a sphero-cylindrical lens occurs through its principal power meridians. The tangential error is the error from the desired focus through the tangential meridian of the lens as a result of lens aberrations. The sagittal error is the error from the desired focus through the sagittal meridian of the lens.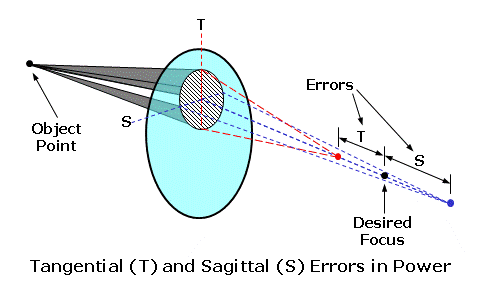

Oblique Astigmatism

Oblique astigmatism is an aberration that results when rays of light from an object in the periphery strike the lens obliquely, and are refracted differently by the tangential and sagittal meridians of the lens. When a lens suffers from oblique astigmatism, the tangential meridian (T) of the lens refracts incident light more than the sagittal meridian (S) perpendicular to it. Consequently, incident light from an off-axis object point is brought to a focus at two different locations (i.e., the tangential focus and the sagittal focus). The image of the object point is no longer focused to a single point, but rather separated into two focal lines instead.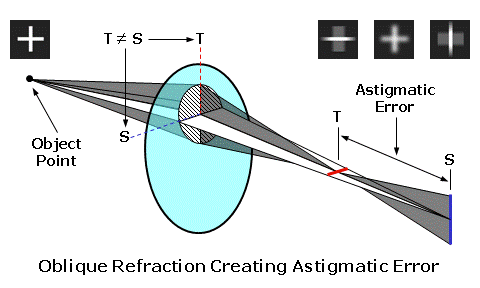

Note that two focal lines are produced from each single object point by the tangential and sagittal meridians of the lens, instead of a single point focus. The dioptric difference between these two focal lines is known as the astigmatic error of the lens. Oblique astigmatism is similar to the normal ocular astigmatism for which refractionists prescribe cylinder power. However, oblique astigmatism only occurs when the wearer looks through the lens at an angle (hence, "oblique") or through the peripheral regions of the lens. Since it is an astigmatic focusing error, this error is similar in effect to unwanted cylinder power in a prescription.

When light is incident upon a surface at an angle, it produces such an astigmatic focus. Since light is refracted by two surfaces as it passes through a lens, the total oblique astigmatism produced by the lens depends upon the net astigmatism produced at each surface. Consequently, oblique astigmatism is dependent upon the form of the lens—that is, the relationship between the front and back curves. Certain lens forms will produce more oblique astigmatism than others.

In terms of our tangential and sagittal errors, the astigmatic error is given by:

Astigmatic Error = Tangential Error - Sagittal Error

In addition to the oblique astigmatism that occurs while viewing off-axis objects in the periphery, you can introduce oblique astigmatism by simply tilting a lens, since this also places the line of sight at a significant angle to the optical axis of the lens. This is sometimes referred to as "astigmatism due to lens tilt." The oblique astigmatism induced by lens tilt can be minimized by ensuring that the optical axis of the lens passes through the center of rotation (C) of the eye. We can accomplish this by manipulating the relationship between the pantoscopic tilt—which is lens tilt toward the cheeks—and the height (H) of the wearer's pupil center above the optical center (OC) of the lens according to the following rule-of-thumb:

Ensure 1 mm of Optical Center Drop (H) for Every 2° of Pantoscopic Tilt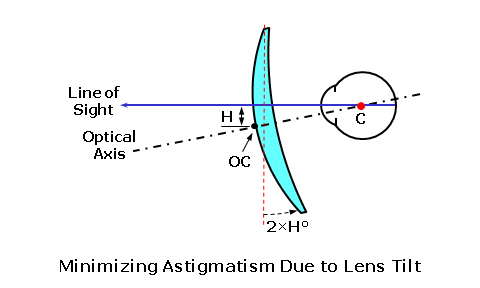

Power Error

In the absence of oblique astigmatism, a spectacle lens brings light to a focus across a curved image plane referred to as the Petzval surface. Curvature of the field is an aberration that results from the difference in focus between a flat focal plane and the curved collection of actual focal points on the Petzval surface. This aberration is a concern for optical devices that require a flat image plane, such as cameras. However, recall that the ideal image plane of the eye, the far-point sphere, is also curved. Unfortunately, the Petzval surface is generally flatter than the far-point sphere. Power error is an aberration that results from the difference in focus between the Petzval surface (PS) and the far-point sphere (FPS) of the eye.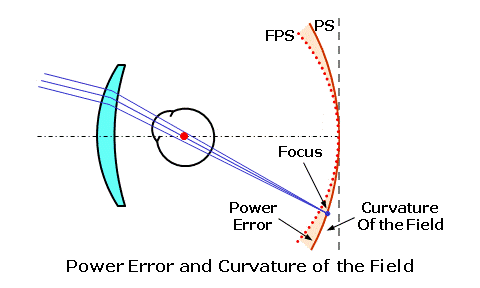

Power error is a result of the fact that the focal plane of the lens for off-axis object points departs from the far-point sphere of the eye, even when the lens is free from oblique astigmatism. In the presence of power error, light from an object point may be refracted to a single point focus by the tangential (T) and sagittal (S) meridians, but this point focus does not lie on the far-point sphere (FPS). The dioptric difference between the actual focal point of the lens and its desired focal point is the power error of the lens. Power error is a spherical-like focusing error, and is similar in effect to unwanted sphere power in a prescription. This is in contrast to the astigmatic error produced by oblique astigmatism.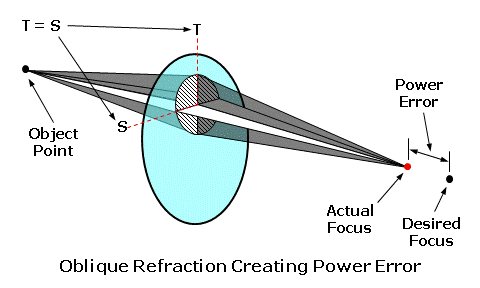

In the presence of oblique astigmatism, there is no single focal point but rather two focal lines. In this case, the power error is equal to the average dioptric difference between the two astigmatic focal lines and the desired focal point of the lens, just as the spherical equivalent is equal to the average power of a sphero-cylindrical prescription.

In terms of our tangential and sagittal errors, the power error is given by:

Power Error = (Tangential Error + Sagittal Error) ÷ 2

For example, consider a +4.00 D lens that produces a power of +5.00 D through the tangential meridian and a power of +4.50 D through the sagittal meridian at some distance from the optical center. This represents a tangential error of 5.00 - 4.00 = +1.00 D and a sagittal error of 4.50 - 4.00 = +0.50 D. The astigmatic error is equal to 1.00 - 0.50 = 0.50 D, while the power error is equal to (1.00 + 0.50) / 2 = +0.75 D.

Other Lens Aberrations

Spherical aberration and coma occur because the focal power of a lens effectively increases away from its optical axis. As a result, rays of light refracted by the peripheral regions of the lens are focused closer to the lens than light rays refracted through the central, paraxial region. Spherical aberration affects rays of light from objects situated near the optical axis, while coma affects rays of light from objects away from the optical axis. The small pupil aperture of the eye minimizes these aberrations by restricting the region of the lens that admits rays of light into the eye at any one time. Conseqently, these two aberrations are generally not a concern for ophthalmic lens designers.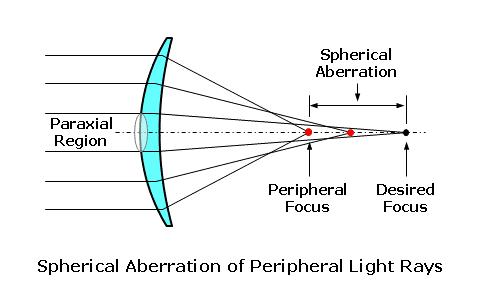

Distortion does not affect the focal quality of an image, but rather its size and shape—or its geometric reproduction. Unlike oblique astigmatism and power error, distortion does not produce a focal error that produces blur. Just as the focal power of a lens effectively increases away from its optical axis, so does the magnification (or minification) produced by the lens. This excess magnification (or minification) causes objects to appear curved or misshapen—particularly in higher powers. Since it cannot be eliminated using conventional base curve ranges, distortion is usually not a consideration for ophthalmic lens design.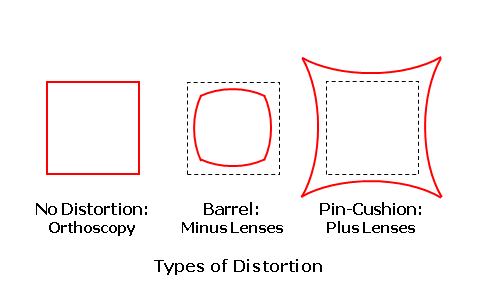

A lens free from distortion exhibits orthoscopy (or no distortion). The excess minification in the periphery of minus lenses generally produces barrel distortion, while the excess magnification of plus lenses generally produces pin-cushion distortion.

Best Form Lens Design

The peripheral vision through a lens that suffers from these lens aberrations is blurred, and the wearer experiences a limited field of clear vision. For conventional lenses, which utilize base curves with spherical surfaces instead of aspheric surfaces, base curve selection is one of the primary tools used to reduce these aberrations.

Recall that amount of oblique astigmatism produced by a lens depends on the relationship between the front and back surfaces (or lens form). When the curves of lens are chosen in an attempt to produce a lens form with a minimum of lens aberrations, the resulting lens is often referred to as a corrected curve lens design. (This term refers to the fact that the base curve has been chosen in order to correct certain aberrations.) Since properly designed corrected curve lenses will have the least amount of the most detrimental aberrations, they are also called best form lens designs.

In 1804, when W. Wollaston experimented with different lens forms to improve peripheral vision. He created a series of lens forms that neutralized the astigmatism produced at the front surface of the lens using the astigmatism produced at the back surface. Essentially, the form was chosen such that the astigmatism produced at the two surfaces canceled each other out. He referred to his lens experimental series as "periscopic," meaning "look around." However, his lens forms turned out to be too steep for practical production as spectacle lenses. In 1898, F. Ostwalt developed another system of lenses free from oblique astigmatism, which were much flatter than Wollaston's.

In 1904, M. Tscherning demonstrated mathematically that there were in fact two recommended or "best form" spherical best curves for each lens power: a steeper series and a flatter series. Wollaston's lenses had been based upon the steeper solutions to Tscherning's formula, while Ostwalt's had been based upon the flatter solutions. Tscherning's ellipse is the locus of points that plot out the two recommended front curves for each lens focal power. The flatter Ostwalt branch of the ellipse serves as the basis for modern best form lenses.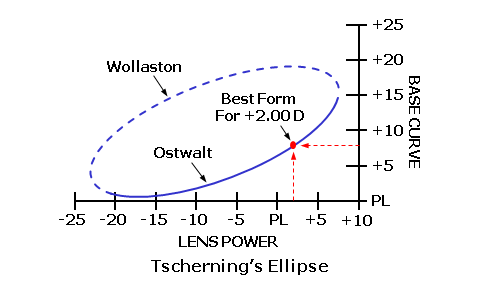

Tshcerning's ellipse indicates the optimum spherical base (or front) curve to use for each lens power in order to reduce or eliminate lens aberrations. For instance, the recommended best form base curve for a lens with +2.00 D of focal power is roughly 8.00 D. After examining Tscherning's ellipse, we can draw a few conclusions:

• Tscherning's ellipse recommends relatively steep base (front) curves for many prescriptions. Unfortunately, the "best form" base curves necessary to provide good peripheral vision also produce relatively steep, thick lens forms. Flatter lens forms, while thinner and lighter, generally produce significant lens aberrations, including large astigmatic and spherical power errors. Consequently, best form lens designs, while optically superior to flatter lens forms, are cosmetically inferior to them.
• The focal power limit of the ellipse is around +7.50 D; above this power, lens aberrations cannot be eliminated without using special, aspheric lens designs.
• According to Tscherning's ellipse, each individual lens power should be made using a separate base curve. Early best form lenses utilized this approach, which required a massive and costly inventory of lens blanks. As stated earlier, manufacturers now group small ranges of prescriptions together upon common lens blanks (that is, base curves) to minimize inventory requirements and keep costs down.

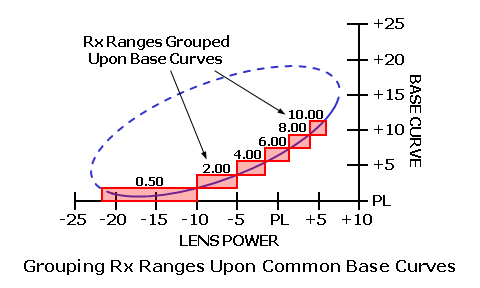This results in somewhat of an optical compromise, but the errors are usually negligible. Nonetheless, the more base curves a given base curve series has, the more precisely the aberrations can be minimized.

It is generally not possible to eliminate all lens aberrations completely. A lens that is entirely free of oblique astigmatism will generally have a small amount of residual power error remaining, and vice versa. It is up to the lens designers of each individual manufacturer to determine which of the two aberrations (or combination thereof) they plan to reduce or eliminate.

Some manufacturers may choose to eliminate oblique astigmatism completely, some may choose to eliminate power completely, and others may choose to eliminate or minimize a combination of the two aberrations. Each of these separate approaches utilizes a slightly different lens form and base curve for each focal power. Consequently, different manufacturers may have slightly different base curve recommendations for their lenses.

The recommended "best form" base curve for a given prescription can be approximated using Vogel's formulas. For plus (+) prescription powers, Vogel's formula is:

Base Curve = Sphere Rx + 6.00

For minus (-) prescription powers, Vogel's formula is:

Base Curve = Sphere Rx / 2 + 6.00

When the prescription also calls for cylinder, use the spherical equivalent—or Sphere + Cylinder / 2. For example, consider a prescription of -4.50 DS -1.00 DC × 180. The spherical equivalent would be -4.50 + (-1.00) / 2 = -5.00. And, since this is a minus prescription, the recommended base curve would be -5.00 / 2 + 6.00 = 3.50.

Vision and Lens Design

Lens aberrations manifest themselves as departures from the desired prescription. For instance, the lens aberrations produced by "flattening" a lens form (i.e., using a base curve that is flatter than recommended) increase the spherical focal power perceived by the wearer in the periphery of the lenses and induce unwanted cylinder power (astigmatism). The result is a change in the effective power of the prescription away from the optical axis (or optical center) of the lens, leaving a "residual" refractive error.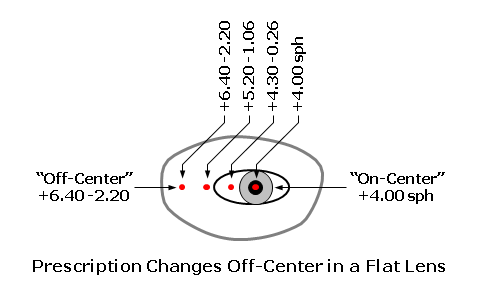

The errors from the desired prescription produced by these lens aberrations result in blurred vision in the periphery and a restricted field of clear vision. Consequently, an imprudently flattened lens design, while thinner and lighter in weight than a "best form" lens design, produces inferior peripheral vision. The best form lens design, on the other hand, offers a wide, clear field of vision.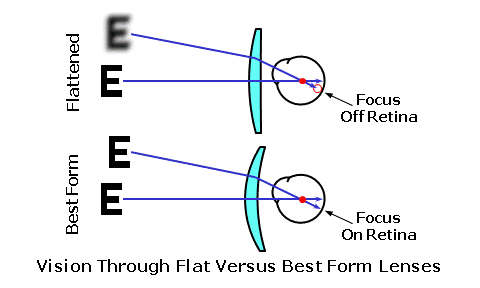

The prescription errors caused by lens aberrations will increase with the following factors:

• Distance from the optical axis/center: The farther the wearer looks into the peripery of a lens, the greater the potential for lens aberrations—and the more rapidly those aberrations will increase.
• Departure from best form design: The farther the lens form departs from the recommended "best form," the greater the potential for lens aberrations.
• Strength of the prescription: The stronger (plus or minus) the focal power of the lens, the greater the potential for lens aberrations.

To summarize, the goal of best form lens design is to determine the most "optically appropriate" base curve for a given focal power (or range of focal powers). This means selecting a base curve that will produce a lens form free from the lens aberrations that can blur vision through the periphery of the lens. This process is referred to as lens design or optimization. When the doctor prescribes a certain prescription, he/she is really specifying the focal power "on-axis." The focal power "off-axis," however, is ultimately controlled by the design of the finished lens.

Asphericity

Best form lenses, although optically superior to flatter lens forms, are somewhat steep, thick, and heavy for many focal powers—at least compared to the flatter lens forms. Does this mean that providing good optics precludes the ability to provide good cosmesis? Fortunately, lens designers have another tool at their disposal when designing lenses: asphericity.

Put simply, an aspheric surface is a surface that departs from being perfectly spherical. Aspheric base curves are surfaces that vary gradually in surface power from the center towards the edge, in a radial fashion (meaning the asphericity is the same in every meridian of the lens—like the spokes of a bicycle wheel).

Unlike a spherical surface, which has the same curvature in any direction across the entire surface, a typical aspheric surface becomes progressively flatter (or, in some cases, steeper) away from the center of the lens—i.e., the tangential meridian of the lens. However, the aspheric surface changes very little around the circumference of the lens, which is the sagittal meridian of the lens perpendicular to the tangential meridian.

This difference in surface curvature (and power) produces surface astigmatism, which means that the surface literally produces cylinder power away from its center. Furthermore, this surface astigmatism is used to counteract and neutralize the oblique astigmatism produced by looking through the lens off-axis. Essentially, the difference in surface power on an aspheric surface cancels out the difference in off-axis focal power produced through the lens by oblique astigmatism. An aspheric surface departs more and more from a spherical surface away from its center, just as oblique astigmatism would normally increase more and more when looking away from the center.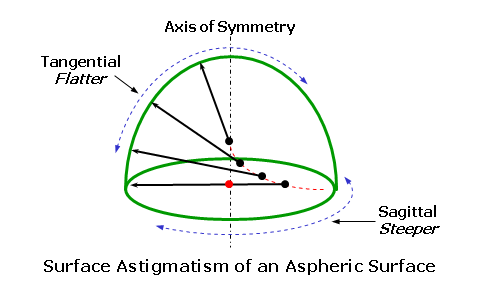

To produce a three-dimensional aspheric surface, an aspheric curve is rotated about an axis of symmetry. As a result, aspheric surfaces are "rotationally-symmetrical." The central region of an aspheric surface will be nearly spherical. Away from this central region, the amount of surface astigmatism smoothly increases towards the periphery of the lens.

In most cases the difference in surface height—or sagitta—between an aspheric curve and a conventional spherical curve results in a thinner profile for aspheric lenses. This means that a lens using an aspheric surface will generally be thinner than a lens using a spherical surface of the same power. Moreover, it is possible to exaggerate the asphericity of a surface in order to maximize cosmesis, though this will generally result in excessive levels of unwanted astigmatism. Some cataract lenses, such as the Welsh 4-Drop, employed such an approach.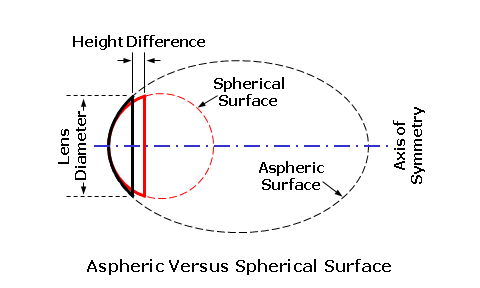

Many aspheric surfaces are made by rotating special curves, called conic sections, around their axis of symmetry. Conic sections include the parabola, the hyperbola, the oblate ellipse, and the prolate ellipse. More general—and sophisticated—aspheric surfaces are described by polynomial equations of the form:

Z = A₂×X² + A₄×X⁴ + A₆×X⁶ ...

where Z is the height of the surface at a distance X from its center and the coefficients A₂, A₄, A₆ ... control the shape of the aspheric surface. This type of surface offers more flexibility to the lens designer than a simple conicoid surface. For instance, the designer may choose to minimize power errors out to a certain point and then exaggerate asphericity to improve cosmesis beyond that point.

Aspheric Lens Design

Asphericity allows lens designers to flatten a lens form in order to improve cosmesis, without sacrificing opical performance. The lens aberrations produced by using flattened lens forms are simply eliminated using the surface astigmatism of the aspheric design. While aspheric lenses do not provide better vision than best form lenses, they do provide equivalent vision in a flatter, thinner, and lighter lens.

Aspheric lenses were originally employed to provide acceptable vision in high-plus, post-cataract lenses that exceeded the +7.50 D limit of Tscherning's ellipse. Today, aspheric surfaces are mainly used to allow lens designers to produce flatter, thinner lenses with the superior optical performance of the steeper corrected curve, or best form, lenses.

Aspheric lenses allow lens designers to produce lenses that are considerably flatter, thinner, and lighter in weight than conventional best form lenses. It is interesting to note that aspheric surfaces produce thinner lenses for two reasons:

• Aspheric lenses generally use flatter front curves, which reduce the center thickness in plus lenses and the edge thickness in minus lenses.
• The geometry of an aspheric surface also provides additional thickness reduction. Some aspheric lenses are even designed solely for cosmesis, and actually use more asphericity than what is optically required. This produces a thinner lens at the expense of reduced optical performance.

As with the base curve of a best form lens, the amount or degree of asphericity will depend upon the focal power of the lens. Additionally, the surface (that is, front or back) upon which the asphericity has been applied will also make a difference:

• Plus lenses. If asphericity is applied to the front surface of a plus lens, the surface will become flatter away from the center. If it is applied to the back surface, the surface will become steeper away from the center.
• Minus lenses. If asphericity is applied to the front surface of a minus lens, the surface will become steeper away from the center. If it is applied to the back surface, the surface will become flatter away from the center.

Ideally, aspheric lenses should be optimized for each individual focal power. In practice, however, small ranges of powers are grouped upon common aspheric base curves—just like with best form lenses. Nevertheless, asphericity gives lens designers the freedom to optimize just about any base (front) curve for the chosen focal power—or range of powers. (Generally, flatter base curves are chosen for cosmesis.)

This is unlike best form lens design, which requires a specific front curve that conforms to Tscherning's ellipse in order to provide good vision for a given focal power. Consequently, before the appropriate aspheric design can be determined, the lens designer must first decide upon the base curve value of the lens blank as well as its intended focal power—or range of focal powers.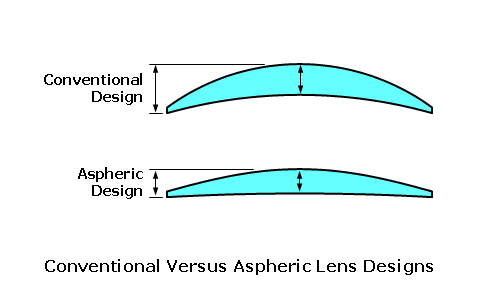

Aspheric base curves free lens designers from the constraints of conventional (best form) lenses, which use simple spherical base curves. Lenses can be made flatter, thinner, and lighter, while maintaining the same excellent optical performance. In summary, aspheric lenses:

• Utilize a non-spherical surface with surface astigmatism to neutralize the oblique astigmatism produced by off-center refraction
• Provide both the visual advantages of best form lenses and the cosmetic advantages of flat lenses
• Do not necessarily provide better optical performance than best form lenses, but simply provide comparable performance without the restrictions imposed by best form base curve selection

The table, below, represents a comparison of lens designs for a +4.00 D prescription in hard resin plastic, edged to a 70-mm diameter and a 1-mm minimum edge thickness. Note that the best form lens design provides good peripheral optics (that is, very little oblique astigmatism off-center), while the flattened lens design (that is, made using a flatter base curve) provides a thinner, lighter, and flatter profile with poor optics. Finally, the aspheric lens design provides both good optics and the thinnest, lightest, and flattest lens profile.

Of course, in some cases it may be desirable to use base or front curves that are actually steeper than "best form" curves. For instance, "wrap" sunwear frames often necessitate highly curved and steeply tilted lenses. Typically, non-standard base curves with a nominal front curve of roughly 8.00 D are chosen for lenses glazed into these frames, resulting in compromised optical performance for many prescriptions. In this case, asphericity can be applied to regain the optical performance, normally afforded by flatter "best form" lenses, using a steeper front curve.

Atoric Lens Design

Tscherning’s ellipse demonstrates that each prescription power requires a unique front curve or lens design in order to achieve optimal optics. A single, rotationally-symmetrical lens surface cannot completely eliminate the power errors produced simultaneously by both principal meridians of sphero-cylindrical lenses with cylinder power. Consequently, standard best form and aspheric lens designs with prescribed cylinder power represent an optical compromise. Lenses must therefore be designed to optimize peripheral optical performance for either the sphere power meridian, the cylinder power meridian, or some power in between the two.

It is possible, however, to eliminate the power errors associated with both the sphere power and cylinder power meridians of sphero-cylindrical lenses using a non-rotationally-symmetrical surface in which the asphericity varies from meridian to meridian. Atoric surfaces have two planes of symmetry corresponding to the principal meridians of the lens, each with a unique amount of asphericity to minimize the peripheral optical aberrations that would otherwise occur through that power meridian. Unlike the change in curvature away from the center of an aspheric lens surface, which remains the same through every radial meridian of the lens, the change in curvature away from the center of an atoric lens surface varies from meridian to meridian.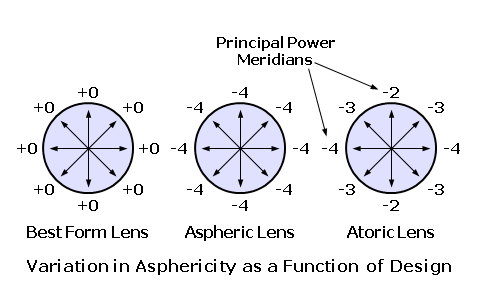

Since any atoricity is most often applied to the toric surface of the lens, atoric can be thought of as a departure from a standard toric surface, just as aspheric refers to a departure from a spherical surface. When the prescription calls for significant cylinder power, the field of clear vision is often restricted through one or more planes of the lens, since a traditional base curve or aspheric lens design can only correct the optical aberrations associated with one power meridian. Atoric lens designs, on the ohter hand, provide unrestricted fields of clear vision, regardless of the power meridian of the lens, since the optical aberrations associated with each power meridian are corrected individually.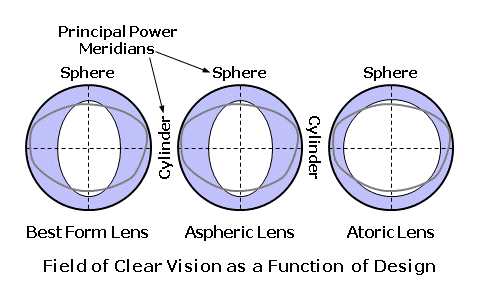