 |
 |
|
|
Chromatic AberrationBy Darryl Meister IntroductionThis course will present the fundamental principles of chromatic aberration, including a review of chromatic dispersion, Abbe value, and techniques to minimize chromatic aberration. This is a technical, intermediate level course intended for dispensing opticians, laboratory technicians, and paraoptometric personnel. An understanding of both basic mathematics and basic optics is required. Visible Light and ColorThe spectrum of electromagnetic radiation includes cosmic rays at one end and radio waves at the other. We think of light as the visible portion of this electromagnetic spectrum. This means that the radiation can stimulate the photoreceptors within the retina of the eye, creating a visual sensation. This region consists of electromagnetic radiation whose waves range from 380 to 760 nanometers (nm)—or one billionth of a meter—in length. This is only 0.000380 to 0.000760 millimeters! The range of radiation visible to the human eye is referred to as the visible spectrum, ranging from violet at one end of the spectrum to red at the other, and represents a small fraction of the total electromagnetic spectrum. 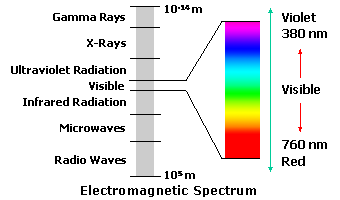 White light is composed of all the wavelengths in the visible spectrum. Individual wavelengths within the visible spectrum, by themselves, create different color sensations. These are the spectral colors. Remember that colors with shorter wavelengths, like blue and violet, have higher frequencies. Beyond the blue end of the visible spectrum lies ultraviolet radiation, while infrared radiation—which is often associated with heat—lies beyond the red end. These two forms of radiation are not visible to the human eye.
Refractive IndexThe substance through which waves of light travel is referred to as the medium. Media can include empty space, air, lens materials, and so on. Recall that waves of light travel at a constant velocity of approximately 300,000 km/s in free space. In other transparent media, including lens materials, waves of light will travel at a slower rate. The velocity of light in other media will vary as a function of the refractive index for that material. The refractive index of a transparent medium is essentially a measure of the "optical resistance" of the material to light, and is defined as the ratio of the velocity of light in air compared to the velocity of light in the material: Refractive Index = Velocity in Air ÷ Velocity in Material For example, consider a wave of light traveling at a velocity of 200,000 km/s through a particular lens material. The refractive index for that lens material would be equal to 300,000 km/s ÷ 200,000 km/s = 1.500. The refractive index of a material is often abbreviated 'n.' Except for air, which has a refractive index of approximately 1, the refractive index of most substances is greater than 1 (n > 1). Water, for instance, has a refractive index of 1.333. The higher the refractive index of a lens material, the slower the light will travel through it. Chromatic DispersionThe higher the refractive index of a lens material, the slower the light will travel through it. In reality, the refractive index of any material varies slightly as a function of the wavelength. This means that various colors of light will each actually have a slightly different refractive index in the same lens material! This phenomenon is responsible for chromatic dispersion, or the breaking up of white light into its component colors by prisms and lenses. Blue light, which has a higher refractive index than red light, is therefore refracted—or bent—more than red light as it passes through a lens or prism. 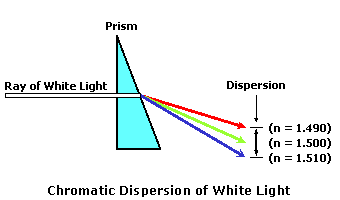 Chromatic dispersion is a result of the fact that colors of light with shorter wavelengths, like blue, travel more slowly through most transparent materials than colors with longer wavelengths, like red. Recall that light at the blue end of the visible spectrum has a higher frequency than light at the red end. Dispersion occurs because waves of light in the blue end of the spectrum are closer to the resonant frequency of the atoms of transparent materials. Resonance is the tendency of a system to absorb more energy when the frequency of its oscillations matches the system's natural frequency of vibration. Because the blue end of the color spectrum is closer to the resonant frequency of lens materials, bluish colors do more "work" and give up more energy than reddish colors, which causes waves of light in the blue end to slow down more. Since the refractive index of a lens material is the ratio of the speed of light in air to the speed of light in the material, bluish colors will have a higher refractive index than reddish colors. The greater the difference between the refractive index of the blue end of the color spectrum and the refractive index of the red end for a given material, the more the material will disperse colors, and vice versa. Moreover, the capability of a lens material to refract light for prisms and lenses is directly related to its refractive index. Consequently, this disperson of colors also means that these colors will be deviated differently through prisms, as well as focused differently through lenses. These difference are referred to as chromatic aberration. For instance, in the presence of chromatic aberration, since blue light has a higher refractive index than red light, blue light will have a shorter focal distance after refraction through a lens. There are actually two categories of chromatic aberration (or dispersion) produced by a spectacle lens:
It is interesting to note that, since the actual refractive index of a lens material will vary from color to color, a single color—or reference wavelength—must be chosen in order to specify the index of a given lens material. In the United States, a wavelength of 587.56 nm is used for specifying the refractive index and power of ophthalmic lenses, which is a yellow-green color produced by electrically excited helium gas. In some countries, 546.07 nm is used as the reference wavelength, which is produced by excited mercury gas. Consequently, the actual power of a lens or prism will depend upon the chosen reference wavelength because of the effects of chromatic aberration. Abbe ValueThe degree to which a given lens material will disperse light is described by a measure of its refractive efficiency or, more commonly, its Abbe value (after Ernst Abbe). It is also referred to as constringence. Lenses with a high Abbe value will disperse light less, and produce less chromatic aberration, than lenses with low Abbe values. Specifically, chromatic aberration is inversely proportional (or inversely related) to the Abbe value. This means that the chromatic aberration of a lens increases as the Abbe value decreases, and vice versa. In general, high-index materials produce lower Abbe values than conventional plastic and crown glass lens materials, which makes these materials more likely to produce symptoms of chromatic aberration. Furthermore, the higher the refractive index of the material, the lower the Abbe value is likey to be. 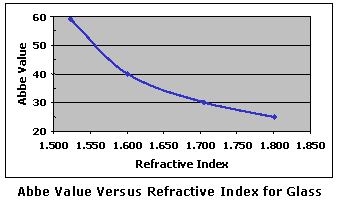 Fortunately, some newer high-index materials have been engineered with higher Abbe values, minimizing this problem. Spectacle lens materials are available in a variety of refractive indices and Abbe values. Some common materials are shown below.
Axial Chromatic AberrationIdeally, a spectacle lens should bring all of the component colors of white light to a single point focus at the focal length of the lens. This means that the lens will refract all of the colors of white light equally, so that they all intersect each other at the same location (or focus). 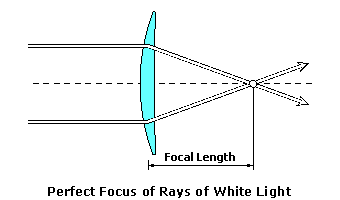 Axial (or longitudinal) chromatic aberration is a measure of the difference in focus between the blue and red ends of the color spectrum caused by chromatic dispersion. Axial chromatic aberration (ACA), in diopters, is calculated by: ACA = Power ÷ Abbe value Axial chromatic aberration results in the blurring of colors that do not fall upon the retina of the eye, which can make certain objects—such as a red "EXIT" sign—look smeared or out of focus. In the presence of axial chromatic aberration, each color of light is brought to a focus at a different distance from the lens, resulting in a separate focal length for each color. Blue light, having the highest refractive index, is refracted more than red light. This means that blue light will have a shorter focal length, or a higher power, than red light through a lens. 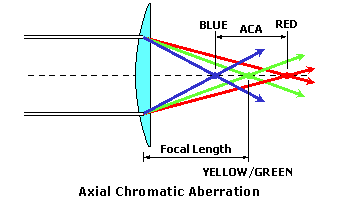 For example, consider a +6.00 D lens made with polycarbonate, which has an Abbe value of 30. The axial chromatic aberration ACA is equal to +6.00 ÷ 30 = 0.20 diopters (D). Lateral Chromatic AberrationLateral (or transverse) chromatic aberration is a measure of the difference in prismatic deviation between the blue and red ends of the color spectrum caused by chromatic dispersion. Lateral chromatic aberration is often the most troublesome of the two aberrations, since its effects are more noticeable under normal circumstances. Lateral chromatic aberration (LCA), in prism diopters (Δ), is calculated by: LCA = Prism ÷ Abbe value Note that prism is given by the power multiplied by the decentration (in centimeters). Lateral axial chromatic aberration results in the familiar "color fringing" around objects. In the presence of lateral chromatic aberration, the various colors of light are prismatically deviated by different amounts. Blue light, having the highest refractive index, is refracted more than red light. This means that blue light will have a greater deviation, or a higher prism amount, than red light through a lens. 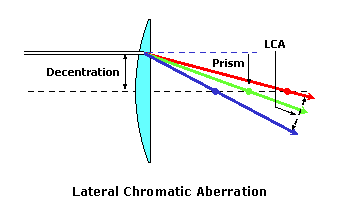 For example, consider a +6.00 D lens made with polycarbonate, which has an Abbe value of 30. At 15 mm (1.5 cm) from the optical center, the prism is +6.00 × 1.5 = 9.0 prism diopters (Δ). The lateral chromatic aberration LCA is equal to 9.0 ÷ 30 = 0.30 Δ. Each color of light creates its own image in the presence of chromatic aberration. Since lateral chromatic aberration deviates each color by a slightly different amount, the image produced by each color is offset slightly from the others. Toward the center of the object, where all of the colors overlap on the retina, the normal object color is observed. However, toward the edges of the object, where the outer colors in the visible spectrum are offset more, a "border" of color is seen. This is the cause of the familiar color fringing around objects that are viewed through the periphery of lenses with chromatic aberration. 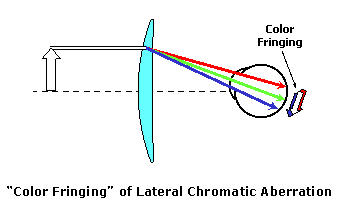 Often, an otherwise white object will show a blue fringe on one side and a red fringe on the other. You can also demonstrate the lateral chromatic aberration of your own eye by slowly sliding a card up over your pupil while staring a bright white object.
Significance of Chromatic AberrationThe human eye suffers from both forms of chromatic aberration, and a typical eye has roughly 1.00 D of axial chromatic aberration. This is actually what allows the common duochrome test to refine a spectacle refraction. A typical spectacle wearer can actually tolerate an appreciable amount of chromatic aberration. Most wearers will not observe color fringing until the lateral chromatic aberration exceeds at least 0.12 prism diopters. In the past, wearer "non-adapt" issues with early high-index lens materials, particularly polycarbonate, were often blamed on chromatic aberration. While the low Abbe value of polycarbonate certainly contributed to visual discomfort in the periphery, other factors may have been equally significant:
Most of these issues have been resolved over the years by advances in technology and an increased understanding of these materials by eyecare professionals. However, when chromatic aberration does become problematic, the color fringing produced by lateral chromatic aberration is generally the first phenomenon observed by wearers. This is particularly true for wearers who try high-index lens materials—which have inherently low Abbe values—for the first time. While wearers often "adapt" to this phenomenon after a week or two, the blur produced by chromatic aberration may continue to impact the quality of vision. Vision scientists have studied the effects of chromatic aberration upon vision, and have demonstrated a relationship between lateral chromatic aberration (LCA) and visual acuity. The following table provides the predicted Snellen visual acuities for a range of lateral chromatic aberration errors (in prism diopters).*
For example, consider another +6.00 D lens made with polycarbonate, which has an Abbe value of 30. At 15 mm (1.5 cm) from the optical center, we have shown that the lateral chromatic aberration LCA = 0.30 Δ. This corresponds to a Snellen visual acuity of 20/31. 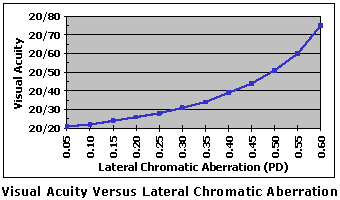 While this small reduction in visual acuity may be just noticeable to the wearer, it is unlikely to elicit an objection. However, the color-fringing produced by lateral chromatic aberration may be troublesome for this wearer until a reasonable adaptation period has passed. * "Effect of Chromatic Dispersion of a Lens on Visual Acuity," Meslin, D. & Obrecht, G. Am. J. of Optom. & Physiol. Optics. 65:25-28, 1988. Minimizing Chromatic AberrationChromatic aberration can be minimized using a variety of techniques. Achromatic doublets, or composite lenses combining a low-index and a high-index lens, are very common in telescopes, mircoscopes, and other precision optical devices. However, these lenses are too complex, too heavy, and too expensive for use as spectacle lenses. Recall that chromatic aberration is directly related to the power of the lens, and inversely related to the Abbe value of the lens material. Consequently, the effects of chromatic aberration are more pronounced in higher-powered lenses or lens materials with lower Abbe values. For spectacle lenses, there are several ways to minimize the effects of chromatic aberration:
Since the amount of color fringing caused by lateral chromatic aberration increases as the prism increases, this illustrates the importance of choosing a well-fitting frame that keeps the lenses nicely centered in front of the eyes. The farther the optical center of the lens is positioned away from the eye, the more prism—and, consequently, lateral chromatic aberration—produced. Of course, this is particularly important when dispensing higher prescriptions or using lens materials with relatively low Abbe values. 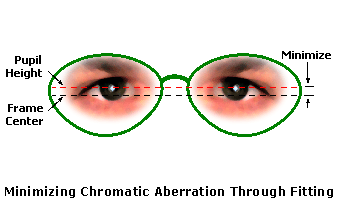 While keeping the wearer's eyes well-centered in the frame will minimize chromatic aberration, specifying "fitting heights" for the optical centers of single vision lenses is generally not recommended. Decentering a single vision lens vertically from the mid-line of the frame to achieve a certain fitting height increases the diameter of the minimum blank size required for the frame, which in turn increases lens thickness. Since high-index lenses, which are the most susceptible to chromatic aberration, are often dispensed because of their slimmer profiles, it is counter-productive to offset the thickness benefits of the higher index by using a larger blank size. |

